已知关于x的方程k2x2-(2k+1)x+1=0有两个不相等的实数根x1、x2.
(1)求k的最小整数值;
(2)若(|x1|-1)(|x2|-1)=-3k,求k的值.
解:(1)∵方程有两个不相等的实数根,
∴△>0,且k≠0,
即(2k+1)
2-4k
2>0,
解得k>-

,
∵k取最小整数,
∴k=1;
(2)∵x
1、x
2是方程两个不相等的实数根,
∴x
1+x
2=-

=
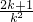
,x
1x
2=

=
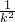
>0,
∴x
1、x
2同号,
∴|x
1|•|x
2|=|x
1x
2|,|x
1|+|x
2|=|x
1+x
2|,
∵(|x
1|-1)(|x
2|-1)=-3k,
∴|x
1x
2|-(|x
1|+|x
2|)+1=-3k,
∴
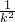
-
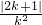
+1=-3k,
由(1)知k>-

,
则|2k+1|=2k+1,
于是可得3k
2+k-2=0,
解得k
1=

,k
2=-1(不合题意,舍去).
分析:(1)根据一元二次方程的根的判别式的符号列出关于k的不等式(2k+1)
2-4k
2>0,且k≠0,通过解该不等式即可求得k的取值范围,由此来确定k的最小整数值;
(2)根据根与系数的关系确定x
1x
2、x
1+x
2的符号,从而去掉绝对值,列出关于k的方程3k
2+k+2=0,通过解方程即可求得k的值.
点评:此题考查了根与系数的关系与根的判别式的知识.此题比较简单,注意掌握根与系数的关系:若一元二次方程x
2+px+q=0的两个根分别是x
1、x
2,则x
1+x
2=-p,x
1•x
2=q.

 ,
, =
=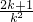 ,x1x2=
,x1x2= =
=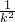 >0,
>0,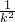 -
-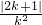 +1=-3k,
+1=-3k, ,
, ,k2=-1(不合题意,舍去).
,k2=-1(不合题意,舍去).
