
【题目】已知,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作
边上一点,作![]() ,分别交边
,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

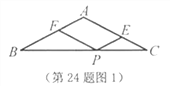
(1)若![]() (如图1),求证:
(如图1),求证:![]() .
.
(2)若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() .试猜想:线段
.试猜想:线段![]() ,
,![]() 和
和![]() 之间的数量关系,并就
之间的数量关系,并就![]() 情形(如图2)说明理由.
情形(如图2)说明理由.
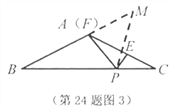
(3)若点![]() 与
与![]() 重合(如图3),
重合(如图3),![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②设![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .
.
【答案】(1)证明见解析;(2)猜想:![]() ,理由见解析;(3)①
,理由见解析;(3)①![]() ;②证明见解析.
;②证明见解析.
【解析】(1)根据平行线的判定,得到![]() ,
,![]() ,证明
,证明![]() .即可证明
.即可证明![]() .
.
(2)过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() ≌
≌![]() 得到
得到![]() .
.
证明四边形![]() 是平行四边形,即可得到
是平行四边形,即可得到![]() .
.
(3)①设![]() ,
,![]() ,根据三角形的内角和列出方程,求解即可.
,根据三角形的内角和列出方程,求解即可.
②延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,证明
,证明 ![]() .根据相似三角形的性质得到
.根据相似三角形的性质得到
![]() ,即可证明.
,即可证明.
【解答】(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
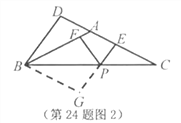
(2)猜想:![]() ,理由如下:
,理由如下:
过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ≌
≌![]() ∴
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
(3)①设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
②延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,
∵![]() ,
,![]() .
.
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60 m到达点C,测得点B在点C的北偏东60°方向,如图②.
(1)求∠CBA的度数;
(2)求出这段河的宽(结果精确到1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).

① ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两棵树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强正在距树AB的20m的点P处从左向右前进,如果小强的眼睛与地面的距离为1.6m,当小强前进多少米时,就恰好不能看到CD的树顶D?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() .
.

(1)如图①,在平面直角坐标系中,以![]() 为顶点,
为顶点,![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() ,若
,若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)如图②,![]() 为
为![]() 轴负半轴上一个动点,以
轴负半轴上一个动点,以![]() 为顶点,
为顶点,![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,当
点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,试问
轴负半轴向下运动时,试问![]() 的值是否发生变化?若不变,求其值,若变化,请说明理由;
的值是否发生变化?若不变,求其值,若变化,请说明理由;
(3)如图③,已知点![]() 坐标为
坐标为![]() ,
,![]() 是
是![]() 轴负半轴上一点,以
轴负半轴上一点,以![]() 为直角边作等腰
为直角边作等腰![]() ,
,![]() 点在
点在![]() 轴上,
轴上,![]() ,设
,设![]() 、
、![]() ,当
,当![]() 点在
点在![]() 轴的负半轴上沿负方向运动时,
轴的负半轴上沿负方向运动时,![]() 的和是否发生变化?若不变,求其值;若变化,请说明理由.
的和是否发生变化?若不变,求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,请按要求画出图形.

(1)画直线AB和射线CB;
(2)连结AC,并在直线AB上用尺规作线段AE,使![]() .(要求保留作图痕迹)
.(要求保留作图痕迹)
(3)在直线AB上确定一点P,使![]() 的和最短,并写出画图的依据.
的和最短,并写出画图的依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
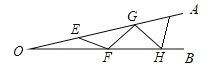
【题目】如图,![]() 是一钢架,且
是一钢架,且![]() ,为使钢架更加牢固,需在其内部添加-一些钢管
,为使钢架更加牢固,需在其内部添加-一些钢管![]() 、
、![]() 、
、![]() ,添加的钢管都与
,添加的钢管都与![]() 相等,则最多能添加这样的钢管( )
相等,则最多能添加这样的钢管( )
A.![]() 根B.
根B.![]() 根C.
根C.![]() 根D.无数根
根D.无数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
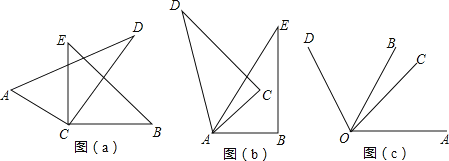
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() .点
.点![]() 是直线
是直线![]() 上方的抛物线上一动点.
上方的抛物线上一动点.
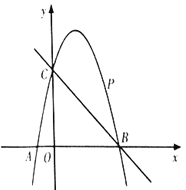
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,
,![]() ,并把
,并把![]() 沿
沿![]() 轴翻折,得到四边形
轴翻折,得到四边形![]() .若四边形
.若四边形![]() 为菱形,请求出此时点
为菱形,请求出此时点![]() 的坐标;
的坐标;
(3)当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com