
【题目】如图,已知点A,B,C,D,请按要求画出图形.

(1)画直线AB和射线CB;
(2)连结AC,并在直线AB上用尺规作线段AE,使![]() .(要求保留作图痕迹)
.(要求保留作图痕迹)
(3)在直线AB上确定一点P,使![]() 的和最短,并写出画图的依据.
的和最短,并写出画图的依据.
科目:初中数学 来源: 题型:
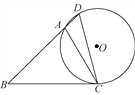
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3![]() ,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
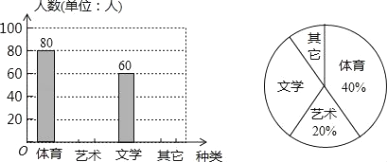
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,顶点
,顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 的高
的高![]() 交线段
交线段![]() 于点
于点![]() ,且
,且![]() .
.
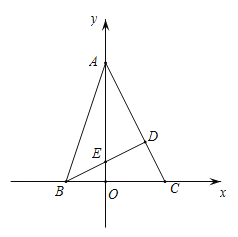
(1)求线段![]() 的长;
的长;
(2)动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以每秒
以每秒![]() 个单位长度的速度运动,
个单位长度的速度运动,![]() 、
、![]() 两点同时出发,且点
两点同时出发,且点![]() 到达
到达![]() 点处时
点处时![]() 、
、![]() 两点同时停止运动,设点
两点同时停止运动,设点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,直接写出相应的
,直接写出相应的![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 是直线
是直线![]() 上的一点且
上的一点且![]() ,是否存在
,是否存在![]() 值,使以点
值,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形与以点
为顶点的三角形与以点![]() 、
、![]() 、
、![]() 为顶点的三角形全等?若存在,请求出符合条件的
为顶点的三角形全等?若存在,请求出符合条件的![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作
边上一点,作![]() ,分别交边
,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

(1)若![]() (如图1),求证:
(如图1),求证:![]() .
.
(2)若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() .试猜想:线段
.试猜想:线段![]() ,
,![]() 和
和![]() 之间的数量关系,并就
之间的数量关系,并就![]() 情形(如图2)说明理由.
情形(如图2)说明理由.
(3)若点![]() 与
与![]() 重合(如图3),
重合(如图3),![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②设![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )

A. 9 B. 10 C. 11 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).
问:(1)设购买乒乓球x盒时,在甲家购买所需多少元?在乙家购买所需多少元?(用含x的代数式表示,并化简)
(2)当购买乒乓球多少盒时,两种优惠办法付款一样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com