
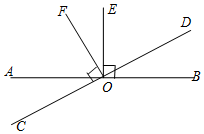
 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.分析 (1)根据余角的定义即可得到结论;
(2)根据余角的定义,对顶角的性质即可得到结论;
(3)根据余角的定义,平角的定义即可得到结论.
解答 解:(1)∵OE⊥AB,OF⊥CD.
∴∠COF+∠AOF=∠AOE+∠AOF=90°,
∵∠AOC=∠BOD,
∴图中∠AOF的余角是∠AOC,∠EOF,∠BOD;
故答案为:∠AOC,∠EOF,∠BOD;
(2)①∠AOC=∠EOF,②∠AOF=∠EOD,③∠EOC=∠BOF;
故答案为:∠AOC=∠EOF,∠AOF=∠EOD,∠EOC=∠BOF;
(3)∵OE⊥AB,OF⊥CD.
∴∠COF+∠AOF=∠AOE+∠AOF=90°,
∴∠AOC=∠EOF,
∵∠AOC=∠BOD,
∴∠BOD=∠EOF,
∴∠AOD+∠BOD=∠AOD+∠EOF=180°,
∴∠AOD=180°-α,
∴∠AOD与∠EOF互补,
∵∠EOF=$\frac{1}{5}$∠AOD,
∴∠EOF=30°.
点评 此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线,所求角与已知角的关系转化求解.


科目:初中数学 来源: 题型:解答题
 如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空
如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空查看答案和解析>>
科目:初中数学 来源: 题型:解答题
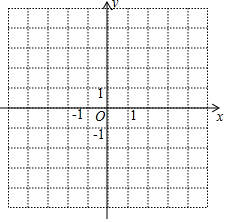 在如图所示的直角坐标系中,△ABC的顶点坐标分别为A(1,-4),B(5,-4),C(4,-1).
在如图所示的直角坐标系中,△ABC的顶点坐标分别为A(1,-4),B(5,-4),C(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届广东省揭阳市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
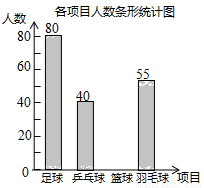
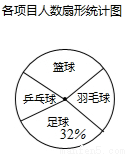
某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com