
【题目】如图,在![]() 中,
中, ![]() ,垂足为
,垂足为![]() ,点
,点![]() 在
在![]() 上,
上, ![]() ,垂足为
,垂足为![]() .
.
(1)![]() 与
与![]() 平行吗?为什么?
平行吗?为什么?
(2)如果![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)平行,理由参见解析;(2)105º.
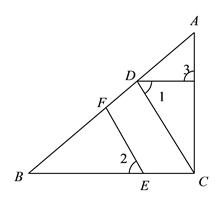
【解析】试题分析:(1)此题考虑平行线的判定方法,找同位角,内错角或同旁内角,利用同位角相等判定,∵CD⊥AB,EF⊥AB,∴∠CDB=∠EFB=90°,∴CD∥EF;(2)利用平行线的性质可得到∠2=∠DCB,∵∠1=∠2,替换:∠1=∠DCB,∴DG∥BC,∴∠ACB=∠3=105°.
试题解析:(1)∵已知CD⊥AB,EF⊥AB,根据垂直的意义,∠CDB=∠EFB=90°,∴CD∥EF(同位角相等,两直线平行);(2)∵CD∥EF,∴∠2=∠DCB(两直线平行,同位角相等),又∵∠1=∠2,∴∠1=∠DCB(等量替换),∴DG∥BC(内错角相等,两直线平行),∴∠ACB=∠3=105°(两直线平行,同位角相等).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图。依据图中信息,解答下列问题:
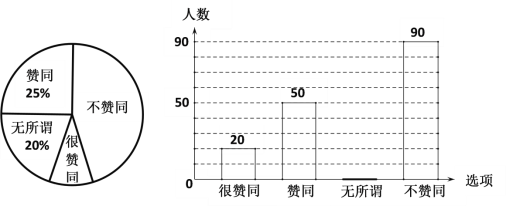
(1)接受这次调查的家长共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“很赞同”的家长占被调查家长总数的百分比是 ;
(4)在扇形统计图中,“不赞同”的家长部分所对应扇形的圆心角度数是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠ACB=90°,点F是AB上一点,作等腰Rt△FCP,且∠PCF=90°,连结AP.
(1)求证:△CFB≌△CPA;
(2)求证:AP2+AF2=PF2;
(3)如图2,在AF上取点E,使∠ECF=45°,求证:AE2+BF2=EF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M点N的距离相等,则x= .
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.一个游戏的中奖概率是 ![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据 8,8,7,10,6,8,9 的众数和中位数都是8
D.若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕![]() )的值;
)的值;
(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com