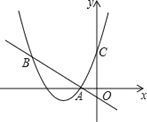
【题目】如图，二次函数的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣2，0）及点B．

（1）求二次函数与一次函数的解析式；

（2）根据图象，写出满足≤kx+b的x的取值范围．

参考答案：

【答案】（1）抛物线解析式为y=x2+6x+8，一次函数解析式为y=﹣2x﹣4；

（2）x的取值范围为﹣6≤x≤﹣2．

【解析】【试题分析】（1）将A（﹣2，0）代入，得0=4-12+n，解得n=8,即抛物线解析式为y=x2+6x+8，当x=0时，y=8,即C(0,8)，且抛物线的对称轴为直线 ，根据B在抛物线上，且与点C关于抛物线的对称轴对称，则点B坐标（﹣6，8）因为y=kx+b经过点A、B，即解得即一次函数解析式为y=﹣2x﹣4.

（2）≤kx+b表示抛物线在一次函数的上方的部分，由图像易得，﹣6≤x≤﹣2．

【试题解析】

（1）∵抛物线经过点A（﹣2，0），

∴. ∴

∴抛物线解析式为y=x2+6x+8

∴点C坐标（0，8）.

∵对称轴x=﹣3，B、C关于对称轴对称，

∴点B坐标（﹣6，8）

∵y=kx+b经过点A、B，

∴解得

∴一次函数解析式为y=﹣2x﹣4.

（2）由图象可知，满足≤kx+b的x的取值范围为﹣6≤x≤﹣2．

关闭