
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0, ![]() ).
).
(1)若此抛物线经过点B(2,-![]() ),且与
),且与![]() 轴相交于点E、F.
轴相交于点E、F.
①填空:b= (用含a的代数式表示);
②当EF的值最小时,求出EF的最小值和抛物线的解析式;
(2)若![]() ,当
,当![]() ,抛物线上的点到x轴距离的最大值为3时,求b的值.
,抛物线上的点到x轴距离的最大值为3时,求b的值.
【答案】(1)①b=-2a-1;②EF有最小值![]() ,抛物线解析式为y=x2﹣3x+
,抛物线解析式为y=x2﹣3x+![]() ;(2)b的值为1或﹣5.
;(2)b的值为1或﹣5.
【解析】试题分析:(1)①由A点坐标可求得c,再把B点坐标代入可求得b与a的关系式,可求得答案;②用a可表示出抛物线解析式,令y=0可得到关于x的一元二次方程,利用根与系数的关系可用a表示出EF的值,再利用函数性质可求得其取得最小值时a的值,可求得抛物线解析式;
(2)可用b表示出抛物线解析式,可求得其对称轴为x=-b,由题意可得出当x=0、x=1或x=-b时,抛物线上的点可能离x轴最远,可分别求得其函数值,得到关于b的方程,可求得b的值.
试题解析:(1)①∵抛物线y=ax2+bx+c的开口向上,且经过点A(0, ![]() ),
),
∴c=![]() ,
,
∵抛物线经过点B(2,-![]() ),
),
∴-![]() =4a+2b+
=4a+2b+![]() ,
,
∴b=-2a-1,
故答案为:-2a-1;
②由①可得抛物线解析式为y=ax2-(2a+1)x+![]() ,
,
令y=0可得ax2-(2a+1)x+![]() =0,
=0,
∵△=(2a+1)2-4a×![]() =4a2-2a+1=4(a-
=4a2-2a+1=4(a-![]() )2+
)2+![]() >0,
>0,
∴方程有两个不相等的实数根,设为x1、x2,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴EF2=(x1-x2)2=(x1+x2)2-4x1x2=![]() =(
=(![]() -1)2+3,
-1)2+3,
∴当a=1时,EF2有最小值,即EF有最小值,
∴抛物线解析式为y=x2-3x+![]() ;
;
(2)当a=![]() 时,抛物线解析式为y=
时,抛物线解析式为y=![]() x2+bx+
x2+bx+![]() ,
,
∴抛物线对称轴为x=-b,
∴只有当x=0、x=1或x=-b时,抛物线上的点才有可能离x轴最远,
当x=0时,y=![]() ,当x=1时,y=
,当x=1时,y=![]() +b+
+b+![]() =2+b,当x=-b时,y=
=2+b,当x=-b时,y=![]() (-b)2+b(-b)+
(-b)2+b(-b)+![]() =-
=-![]() b2+
b2+![]() ,
,
①当|2+b|=3时,b=1或b=-5,且顶点不在范围内,满足条件;
②当|-![]() b2+
b2+![]() |=3时,b=±3,对称轴为直线x=±3,不在范围内,故不符合题意,
|=3时,b=±3,对称轴为直线x=±3,不在范围内,故不符合题意,
综上可知b的值为1或-5.


科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,D是弧AB上一点,C是弧AD的中点,过点C作AB的垂线,交AB
于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①
∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心.其中正确结论是_______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读如下材料.
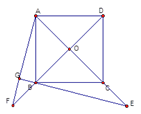
如图,已知正方形ABCD的对角线AC、BD于点O,E是AC上一点,AG⊥BE,垂足为G.求证:OE=OF.
证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,且OA=OE.
又∵AG⊥BE,∴∠1+∠3=90°=∠2+∠3,即∠1=∠2.
∴Rt△BOE≌Rt△AOF,∴OE=OF.

⑴根据你的理解,上述证明思路的核心是利用 使问题得以解决,而证明过程中的关键是证出 .
⑵若上述命题改为:点E在AC的延长线上,AG⊥BE交EB的延长线于点G,延长AG交DB的延长线于点F,如图,其他条件不变.
求证:OF=OE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某自来水公司采取分段计费,每月每户用水不超过10吨,每吨2.2元;超过10吨的部分,每吨加收1.3元.小明家4月份用水15吨,应交水费元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() .(1)直接写出关于
.(1)直接写出关于![]() 的一元二次方程
的一元二次方程![]() 的两个根;
的两个根;

(2)试判断:抛物线![]() 的顶点
的顶点![]() 在第几象限内;
在第几象限内;
(3)过点A的直线y=x+m与抛物线![]() 相交于另一点B,抛物线
相交于另一点B,抛物线![]() 的对称轴与x轴相交于C.试问:在抛物线上是否存在一点D,使
的对称轴与x轴相交于C.试问:在抛物线上是否存在一点D,使![]() ?若存在,求抛物线的表达式,若不存在,说明理由。
?若存在,求抛物线的表达式,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
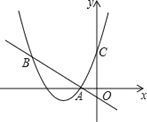
【题目】如图,二次函数![]() 的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣2,0)及点B.
的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣2,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足![]() ≤kx+b的x的取值范围.
≤kx+b的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com