
����Ŀ�����Ķ����²���.
��ͼ����֪������ABCD�ĶԽ���AC��BD�ڵ�O��E��AC��һ�㣬AG��BE������ΪG.��֤��OE=OF.
֤�������ı���ABCD��������.
���BOE=��AOF=90��,��OA=OE.
�֡�AG��BE�����1+��3��90������2+��3������1����2.
��Rt��BOE��Rt��AOF,��OE=OF.

�Ÿ���������⣬����֤��˼·�ĺ��������� ʹ������Խ������֤�������еĹؼ���֤�� .
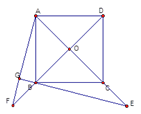
�������������Ϊ����E��AC���ӳ����ϣ�AG��BE��EB���ӳ����ڵ�G���ӳ�AG��DB���ӳ����ڵ�F����ͼ��������������.
��֤��OF=OE.
���𰸡���������ȫ�ȣ���1����2����2����������
�������������������1�����������εĶԽ�������ҡ����ഹֱƽ��֤������1=��2���ٸ���AAS֤����Rt��BOE��Rt��AOF������ȫ����ȫ�ȵ����ʼ���֤��OE=OF��
��2�����������ε��ı���ȣ�ÿ���Խ���ƽ��һ��Խǣ�֤������ABF=��BCE���Ӷ�֤������ABF�ա�BCE������ȫ����ȫ�ȵ����ʼ���֤��OE=OF.
�����������1������֤��˼·�ĺ���������ȫ�������ε�����ʹ������Խ������֤�������еĹؼ���֤����1=��2��
�ʴ�Ϊ��ȫ�������ε�����ʹ������Խ������1=��2.
��2����ABCD����������
���ABO=��ACB=45�� ��AB=BC�� OB=OC��
���ABF=��BCE=135�� ��
�ߡ�OAF+��F=90�� ����OAF+��E=90����
���ABF�ա�BCE(AAS)
��BF=CE��
��BF+OB=CE+OC����OE=OF.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ձ�ȫ����������������ڼ䣬����ij�ձ���ƽ��ÿ�������300���ձ�������1���ձ���������1Ԫ�������鷢�֣����۵���ÿ��0.1Ԫ��ƽ��ÿ��ɶ�����100����Ϊ��ʹÿ���ȡ��������࣬�õ���������۵����½�m��0��m��1��Ԫ
��1�����۵����½�mԪ��ÿ���ձ�������Ϊ����Ԫ���õ�ƽ��ÿ��������������ձ����ú�m�Ĵ���ʽ��ʾ���軯��
��2���ڲ������������ص������£���m��Ϊ����ʱ������ʹ�õ�ÿ���ȡ��������420Ԫ�����������ձ����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A������ƽ��3����λ���ȣ�������ƽ��4����λ���ȣ��õ���A����3��6�������A������Ϊ�� ��
A. ��7��3��B. ��7��3��C. ��6��10��D. ��1��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ͬʱ��ʼ�ӹ�һ����װ���ӿ�ʼ�ӹ����ӹ���������װ�׳��乤����9Сʱ���ҳ�������;ͣ��һ��ʱ��ά���豸��Ȼ��ͣ��ǰ�Ĺ���Ч�ʼ����ӹ���ֱ����׳���ͬʱ���������װ�ļӹ�����Ϊֹ����ס�����������Լӹ���װ������Ϊy���������׳���ӹ���ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ��
��1���׳���ÿСʱ�ӹ���װ����Ϊ�� ������������װ���ܼ���Ϊ�� ������
��2�����ҳ���ά���豸���ҳ���ӹ���װ����y��x֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3����ס��������乲ͬ�ӹ���1000����װʱ�׳������õ�ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ�100�����ݽ�������������Ƶ���ֲ����У������Ƶ��֮�͵���______�������Ƶ��֮�͵���_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c�Ŀ������ϣ��Ҿ�����A(0, ![]() ).
).
��1�����������߾�����B��2��-![]() ��������
��������![]() ���ཻ�ڵ�E��F.
���ཻ�ڵ�E��F.
����գ�b= ���ú�a�Ĵ���ʽ��ʾ����
�ڵ�EF��ֵ��Сʱ�����EF����Сֵ�������ߵĽ���ʽ��
��2����![]() ����
����![]() ���������ϵĵ㵽x���������ֵΪ3ʱ����b��ֵ.
���������ϵĵ㵽x���������ֵΪ3ʱ����b��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����=60�㣬������������࣬����������������������ֵ���ڣ�������
A. 30��B. 60��C. 120��D. 150��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com