
| A. | 如果两个数的绝对值相等,那么这两个数相等 | |
| B. | 两直线平行,内错角相等 | |
| C. | 矩形的四个角都相等 | |
| D. | 对顶角相等 |
分析 先交换各命题的题设与结论部分得到四个逆命题,然后分别根据绝对值的意义、平行线的判定、矩形的判定方法和对顶角的定义判断逆命题的真假.
解答 解:A、逆命题为:如果两个数相等,那么这两个数的绝对值相等,此逆命题为真命题;
B、逆命题为内错角相等,两直线平行,此逆命题为真命题;
C、逆命题为:四个角都相等的四边形为矩形,此逆命题为真命题;
D、逆命题为:相等的角为对顶角,此逆命题为假命题.
故选D.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理. 也考查了逆命题.


科目:初中数学 来源: 题型:选择题
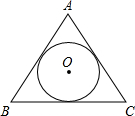 如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )
如图,若等边△ABC的内切圆⊙O的半径是2,则△ABC的面积是( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
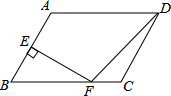 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )| A. | 2$\sqrt{13}$ | B. | 8 | C. | 5$\sqrt{2}$ | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=1,b2=2,c2=3 | B. | a:b:c=3:4:5 | C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=3:4:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com