
���� ��1���������⣬���ȸ��ݶ�������д��һ�ԡ����������ߡ����ɣ�
��2���ȸ����������a1��b1��c1��ֵ�����ú���k�Ĵ���ʽ�Ѻ���y2��ʾ�����������ý⣻
��3�������������䷽��д�ɶ���ʽ�����ɵý⣮
��� �⣺��1��y=x2+x+1��y=2x2+2x+2��
��2��������ã�$\left\{\begin{array}{l}{-\frac{{b}_{1}}{{2a}_{1}}=1}\\{5{=9a}_{1}{+3b}_{1}{+c}_{1}}\\{8{=c}_{1}}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{{a}_{1}=-1}\\{{b}_{1}=2}\\{{c}_{1}=8}\end{array}\right.$��
��${y}_{1}={-x}^{2}+2x+8$��
��${y}_{2}=\frac{{-x}^{2}}{k}+\frac{2x}{k}+\frac{8}{k}$��
��${y}_{1}+{y}_{2}=��-1-\frac{1}{k}��{x}^{2}+��2+\frac{2}{k}��x+��8+\frac{8}{k}��$
=$��-1-\frac{1}{k}����x-1��^{2}+9+\frac{9}{k}$��
��9+$\frac{9}{k}$=-9��
��ã�k=$-\frac{1}{2}$��
��${y}_{2}=2{x}^{2}-4x-16$��
��3��${y}_{1}+{y}_{2}={x}^{2}-2x-8$
=��x-1��2-9��
�����߿������ϣ��Գ���Ϊֱ��x=1��
��x��1ʱ��y��x���������С��
����-3��x��-1��Χ�ڣ���x=-1ʱ��y1+y2����СֵΪ-5��
���� ������Ҫ�����˶��κ����Ķ��������ʣ��Լ�ѧ������ѧ������������������ǽ���Ĺؼ���ע���ܽᣮ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 90�� | C�� | 120�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ľ���ֵ��ȣ���ô����������� | |
| B�� | ��ֱ��ƽ�У��ڴ������ | |
| C�� | ���ε��ĸ��Ƕ���� | |
| D�� | �Զ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4cm��6cm | B�� | 6cm��8cm | C�� | 20cm��30cm | D�� | 8cm��12cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
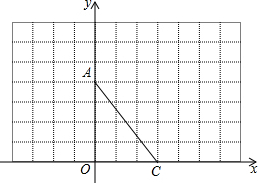 ��ͼ����ֱ������ϵ�У�A��0��4����C��3��0����
��ͼ����ֱ������ϵ�У�A��0��4����C��3��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
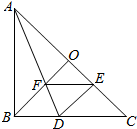 ��ͼ����Rt��ABC�У�AB=CB��BO��AC���ѡ�ABC�۵���ʹAB����AC�ϣ���B��AC�ϵĵ�E�غϣ�չ�����ۺ�AD��BO�ڵ�F������DE��EF�����н��ۣ���tan��ADB=2����ͼ����4��ȫ�������Σ���BD=BF����S�ı���DFOE=S��AOF����������DEF��EF�۵������Dһ������AC�ϣ�������������ȷ�ĸ����ǣ�������
��ͼ����Rt��ABC�У�AB=CB��BO��AC���ѡ�ABC�۵���ʹAB����AC�ϣ���B��AC�ϵĵ�E�غϣ�չ�����ۺ�AD��BO�ڵ�F������DE��EF�����н��ۣ���tan��ADB=2����ͼ����4��ȫ�������Σ���BD=BF����S�ı���DFOE=S��AOF����������DEF��EF�۵������Dһ������AC�ϣ�������������ȷ�ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.2��108 | B�� | 12��108 | C�� | 1.2��10-9 | D�� | 1.2��109 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com