
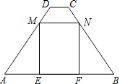
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上运动,并保持
上运动,并保持![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .四边形
.四边形![]() 面积的最大值是( )
面积的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
作梯形ABCD的高DG、CH,先通过梯形两底的差和腰的长求出DG=4,再证明△MEA≌△NFB,得到AE=BF,设AE=x,则EF=7-2x,根据△MEA∽△DGA,求出![]() ,根据矩形的面积公式得出S矩形MEFN和x的关系式,化成顶点式即可求出答案.
,根据矩形的面积公式得出S矩形MEFN和x的关系式,化成顶点式即可求出答案.
如图,分别过D,C两点作DG⊥AB于点G,CH⊥AB于点H.

∵AB∥CD,
∴DG=CH,DG∥CH.
∴四边形DGHC为矩形,GH=CD=1.
∵DG=CH,AD=BC,∠AGD=∠BHC=90°,
∴△AGD≌△BHC(HL),
∴![]()
∵在Rt△AGD中,AG=3,AD=5,
∴DG=4.
∵MN∥AB,ME⊥AB,NF⊥AB,
∴∠MEF=90°,
∴ME=NF,ME∥NF,
∴四边形MEFN为矩形.
∵AB∥CD,AD=BC,
∴∠A=∠B.
∵ME=NF,∠MEA=∠NFB=90°,
∴△MEA≌△NFB(AAS).
∴AE=BF,
设AE=x,则EF=7-2x,
∵∠A=∠A,∠MEA=∠DGA=90°,
∴△MEA∽△DGA,
∴![]()
∴![]()
S矩形MEFN=![]()
当![]() 时,ME=
时,ME=![]()
∴四边形MEFN面积的最大值为![]() .
.
故选:C.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,∠A=∠B=90°,AB=![]() ,点E在AB上,∠AED=45°,DE=6,CE=7.
,点E在AB上,∠AED=45°,DE=6,CE=7.
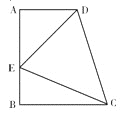
(1)求AE的长;
(2)求sin∠BCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
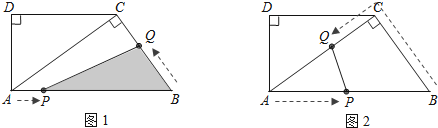
【题目】如图1,DC∥AB,∠D=90°,AC⊥BC,AB=10cm,BC=6cm. 点P以1cm/s的速度从点A出发,沿AB方向向点B运动,同时点Q以2cm/s的速度从点B出发,沿B→C→A方向向点A运动,当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)① 求证:△ACD∽△BAC;② 求DC的长;
(2)当点Q在边BC上运动,求t为何值时,△PBQ的面积为![]() cm2;
cm2;
(3)如图2,当点Q在边CA上运动,求t为何值时,PQ∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .按照以下步骤作图:①以点
.按照以下步骤作图:①以点![]() 为圆心,以适当的长为半径作弧,分别交
为圆心,以适当的长为半径作弧,分别交![]() 的两边于
的两边于![]() 两点,连接
两点,连接![]() .②分别以点
.②分别以点![]() 为圆心,以大于线段
为圆心,以大于线段![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点
内交于点![]() ,连接
,连接![]() .③连接
.③连接![]() 交
交![]() 于点
于点![]() .下列结论中错误的是( )
.下列结论中错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
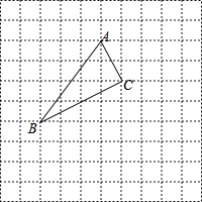
【题目】 如图,把△ABC放置在每个小正方形边长为1的网格中,点A,B,C均在格点上,建立适当的平面直角坐标系xOy,使点A(1,4),△ABC与△A'B'C'关于y轴对称.
(1)画出该平面直角坐标系与△A'B'C';
(2)在y轴上找点P,使PC+PB'的值最小,求点P的坐标与PC+PB'的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,四边形
的直径,四边形![]() 是内接正方形.
是内接正方形.
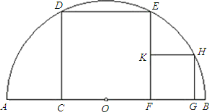
(1)求证:![]() ;
;
(2)在正方形![]() 的右侧有一正方形
的右侧有一正方形![]() ,点
,点![]() 在
在![]() 上,
上,![]() 在半圆上,
在半圆上,![]() 在
在![]() 上.若正方形
上.若正方形![]() 的边为
的边为![]() ,求正方形
,求正方形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书, 于是又折回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
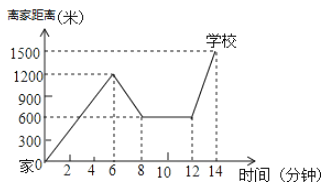
(1)小明家到学校的距离是__ _米;
(2)小明在书店停留了 分钟;
(3)本次上学途中,小明一共骑行了 米;
(4)我们认为骑车的速度超过了![]() 米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由,
米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
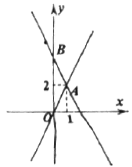
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据查结果,把学生的安全意识分成淡薄、一般、较强、很强四个层次,并绘制成如下两幅尚不完整的统计图:

根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为淡薄、一般的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请将条形统计图补充完整.
(3)求出安全意识为“较强”的学生所占的百分比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com