
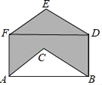
【题目】如图是由射线![]() 组成的平面图形,则
组成的平面图形,则![]() +
+![]() +
+![]() +
+![]() +
+![]() =_____.
=_____.

【答案】360°
【解析】分析:首先根据图示,可得∠1=180°-∠BAE,∠2=180°-∠ABC,∠3=180°-∠BCD,∠4=180°-∠CDE,∠5=180°-∠DEA,然后根据三角形的内角和定理,求出五边形ABCDE的内角和是多少,再用180°×5减去五边形ABCDE的内角和,求出∠1+∠2+∠3+∠4+∠5等于多少即可.
详解:∠1+∠2+∠3+∠4+∠5
=(180°-∠BAE)+(180°-∠ABC)+(180°-∠BCD)+(180°-∠CDE)+(180°-∠DEA)
=180°×5-(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)
=900°-(5-2)×180°
=900°-540°
=360°.
故答案为:360°.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC,若△ABC的边长为4,AE=2,则BD的长为( )

A. 2 B. 3 C. ![]() D.
D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CBD、∠BCE是△ABC的外角,BP平分∠ABC,CP平分∠ACB,BQ平分∠CBD,CQ平分∠BCE.
(1)∠PBQ的度数是 ,∠PCQ的度数是 ;
(2)若∠A=70°,求∠P和∠Q的度数;
(3)若∠A=α,则∠P= ,∠Q= (用含α的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)
如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)
(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)
(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程;
(拓展引申)
(3)如图4,在(1)的条件下,M是AB边上任意一点(不含端点A、B),N是射线BD上一点,且AM=BN,连接MN与BC交于点Q,这个数学兴趣小组经过多次取M点反复进行实验,发现点M在某一位置时BQ的值最大.若AC=BC=4,请你直接写出BQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=4cm,AC=3cm.将△ABC沿着与AB垂直的方向向上平移3cm,得到△DEF.
(1)四边形ABDF是什么四边形?
(2)求阴影部分的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.
(1)作![]() 的平分线
的平分线![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() .
.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
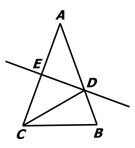
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为14,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC

①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com