
ШчЭМЃЌвбжЊХзЮяЯп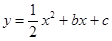 гыxжсНЛгкAЃЌBСНЕуЃЌЖдГЦжсЮЊжБЯп
гыxжсНЛгкAЃЌBСНЕуЃЌЖдГЦжсЮЊжБЯп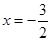 ЃЌжБЯпADНЛХзЮяЯпгкЕуDЃЈ2ЃЌ3ЃЉЃЎ
ЃЌжБЯпADНЛХзЮяЯпгкЕуDЃЈ2ЃЌ3ЃЉЃЎ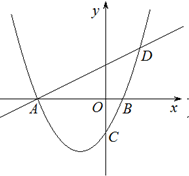
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвбжЊЕуMЮЊЕкШ§ЯѓЯоФкХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЕБЕуMдкЪВУДЮЛжУЪБЫФБпаЮAMCOЕФУцЛ§зюДѓЃПВЂЧѓГізюДѓжЕЃЛ
ЃЈ3ЃЉЕБЫФБпаЮAMCOУцЛ§зюДѓЪБЃЌЙ§ЕуMзїжБЯпЦНаагкyжсЃЌдкетЬѕжБЯпЩЯЪЧЗёДцдквЛИівдQЕуЮЊдВаФЃЌOQЮЊАыОЖЧвгыжБЯпBCЯрЧаЕФдВЃПШєДцдкЃЌЧѓГідВаФQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊ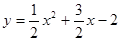 .ЁЁ
.ЁЁ
(2) ЕБЕуMЮЊ(Ѓ2ЃЌЃ3)ЪБЫФБпаЮAMCOУцЛ§газюДѓжЕЃЌзюДѓжЕЮЊ8ЃЎ
(3) ДцдквЛИівдQЕуЮЊдВаФЃЌOQЮЊАыОЖЧвгыжБЯпBCЯрЧаЕФдВЃЌЕуQЕФзјБъЮЊЃЈЉ2ЃЌ4ЃЉЛђЃЈЉ2ЃЌЉ1ЃЉЃЎЁЁЁЁ
НтЮіЪдЬтЗжЮіЃКЃЈ1ЃЉгЩД§ЖЈЯЕЪ§ЗЈМДПЩЕУЃЛ
ЃЈ2ЃЉСЌНгOMЃЌдђЫФБпаЮAMCOПЩЗжЮЊСНИіШ§НЧаЮЃЌЩшMЕуЕФзјБъЃЌдђПЩБэЪОГіСНИіШ§НЧаЮЕФУцЛ§ЃЌНјЖјПЩЕУЕНУцЛ§ЕФзюДѓжЕ
ЃЈ3ЃЉПЩвдЯШМйЩшДцдкетбљЕФЕуЃЌШЛКѓИљОнЬтжаЕФЬѕМўНјааМЦЫуМДПЩ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯп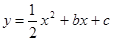 ЕФЖдГЦжсЪЧжБЯп
ЕФЖдГЦжсЪЧжБЯп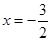 ,
,
Ёр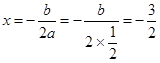 ЃЌНтЕУ
ЃЌНтЕУ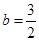 .
.
ЁпХзЮяЯп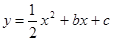 ОЙ§D(2,3),
ОЙ§D(2,3),
Ёр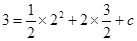 ЃЌНтЕУ
ЃЌНтЕУ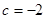 .
.
ЁрХзЮяЯпЕФНтЮіЪНЮЊ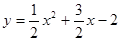 .
.
ЃЈ2ЃЉХзЮяЯпЕФНтЮіЪНЮЊЃК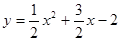 ,
,
СюxЃН0ЃЌЕУyЃНЉ2ЃЌЁрCЃЈ0ЃЌ -2ЃЉЃЎ
СюyЃН0ЃЌЕУxЃНЉ4Лђ1ЃЌЁрA(-4ЃЌ0)ЁЂBЃЈ1ЃЌ0ЃЉЃЎ
ЩшЕуMзјБъЮЊ(mЃЌ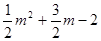 )ЃЌСЌНгMOЃЎ
)ЃЌСЌНгMOЃЎ
дђSЫФБпаЮAMCOЃНSЁїAMOЃЋSЁїCMO
ЃН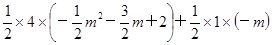
ЃН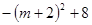
ЁрЕБmЃНЉ2ЪБЃЌ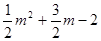 ЃНЃ3
ЃНЃ3
ЁрЕБЕуMЮЊ(Ѓ2ЃЌЃ3)ЪБЫФБпаЮAMCOУцЛ§газюДѓжЕЃЌзюДѓжЕЮЊ8ЃЎЁЁЁЁ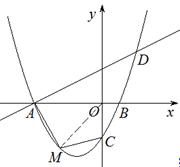
ЃЈ3ЃЉМйЩшДцдкетбљЕФЁбQЃЎ
ЩшжБЯпxЃНЉ2гыxжсНЛгкЕуGЃЌгыжБЯпBCНЛгкЕуFЃЎЩшжБЯпBCЕФНтЮіЪНЮЊyЃНkxЃЋbЃЌ
НЋBЃЈ1ЃЌ0ЃЉЁЂCЃЈ0ЃЌЉ2ЃЉДњШыЕУЃК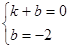 ЃЌНтЕУЃКkЃН2ЃЌbЃНЉ2ЃЌ
ЃЌНтЕУЃКkЃН2ЃЌbЃНЉ2ЃЌ
ЁржБЯпBCНтЮіЪНЮЊЃКyЃН2xЉ2ЃЌ
СюxЃНЉ2ЃЌЕУyЃНЉ6ЃЌЁрFЃЈЉ2ЃЌЉ6ЃЉЃЌGFЃН6ЃЎ
дкRtЁїBGFжаЃЌгЩЙДЙЩЖЈРэЕУЃК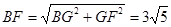 ,
,
ЩшQЃЈЉ2ЃЌnЃЉЃЌдђдкRtЁїQGOжаЃЌгЩЙДЙЩЖЈРэЕУЃК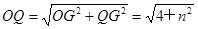 .
.
ЩшЁбQгыжБЯпBCЯрЧагкЕуEЃЌдђQEЃНOQЃН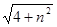 ЃЎ
ЃЎ
дкRtЁїBGFгыRtЁїQEFжаЃЌ
ЁпЁЯBGFЃНЁЯQEFЃН90ЁуЃЌЁЯBFGЃНЁЯQFEЃЌ
ЁрRtЁїBGFЁзRtЁїQEF.
Ёр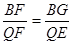 ЃЌМД
ЃЌМД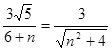 .
.
ЛЏМђЕУЃКn2Љ3nЉ4ЃН0ЃЌНтЕУnЃН4ЛђnЃНЉ1ЃЎ
ЁрДцдквЛИівдQЕуЮЊдВаФЃЌOQЮЊАыОЖЧвгыжБЯпBCЯрЧаЕФдВЃЌЕуQЕФзјБъЮЊЃЈЉ2ЃЌ4ЃЉЛђЃЈЉ2ЃЌЉ1ЃЉЃЎ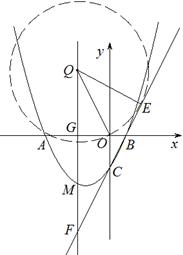
ПМЕуЃК1ЁЂД§ЖЈЯЕЪ§ЗЈЃЛ2ЁЂЖўДЮКЏЪ§ЕФаджЪЃЛ3ЁЂЙДЙЩЖЈРэЃЛ4ЁЂЧаЯпЕФаджЪ


 УћаЃСЗПМОэЦкФЉГхДЬОэЯЕСаД№АИ
УћаЃСЗПМОэЦкФЉГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
дкЦНУцжБНЧзјБъЯЕжаЃЌНЋХзЮяЯп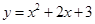 ШЦзХЫќгыyжсЕФНЛЕуа§зЊ180ЁуЃЌЫљЕУХзЮяЯпЕФНтЮіЪНЮЊ ЃЎ
ШЦзХЫќгыyжсЕФНЛЕуа§зЊ180ЁуЃЌЫљЕУХзЮяЯпЕФНтЮіЪНЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
вбжЊЖўДЮКЏЪ§ ЕФЭМЯѓШчЭМЫљЪОЃЌгаЯТСа5ИіНсТлЃК
ЕФЭМЯѓШчЭМЫљЪОЃЌгаЯТСа5ИіНсТлЃК
ЂйabcЃМ0ЃЛЂкbЃМaЃЋcЃЛЂл4aЃЋ2b+c>0ЃЛЂм2cЃМ3bЃЛЂнaЃЋbЃМm (amЃЋb)ЃЈmЁй1ЕФЪЕЪ§ЃЉЁЃ
Цфжае§ШЗНсТлЕФађКХгаЁЁ ЁЁЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
вбжЊжБЯпy=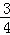 xЉ3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпy=Љ
xЉ3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпy=Љ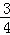 x2+mx+nОЙ§ЕуAКЭЕуCЃЎ
x2+mx+nОЙ§ЕуAКЭЕуCЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкжБЯпCAЩЯЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуDЃЌЪЙЕУЁїACDЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ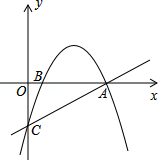
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ШчЭМЃЌЖўДЮКЏЪ§y=x2+bx+cОЙ§ЕуЃЈ-1ЃЌ0ЃЉКЭЕуЃЈ0ЃЌ-3ЃЉЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЙћвЛДЮКЏЪ§y=4x+mЕФЭМЯѓгыЖўДЮКЏЪ§ЕФЭМЯѓгаЧвжЛгавЛИіЙЋЙВЕуЃЌЧѓmЕФжЕКЭИУЙЋЙВЕуЕФзјБъЃЛ
ЃЈ3ЃЉНЋЖўДЮКЏЪ§ЭМЯѓyжсзѓВрВПЗжбиyжсЗелЃЌЗелКѓЕУЕНЕФЭМЯѓгыдЭМЯѓЪЃгрВПЗжзщГЩвЛИіаТЕФЭМЯѓЃЌИУЭМЯѓМЧЮЊGЃЌШчЙћжБЯпy=4x+nгыЭМЯѓGга3ИіЙЋЙВЕуЃЌЧѓnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌМКжЊЕуOЃЈ0ЃЌ0ЃЉЃЌAЃЈ5ЃЌ0ЃЉЃЌBЃЈ4ЃЌ4ЃЉЃЎ
ЃЈ1ЃЉЧѓЙ§OЁЂBЁЂAШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉдкЕквЛЯѓЯоЕФХзЮяЯпЩЯДцдкЕуMЃЌЪЙвдOЁЂAЁЂBЁЂMЮЊЖЅЕуЕФЫФБпаЮУцЛ§зюДѓЃЌЧѓЕуMЕФзјБъЃЎ
ЃЈ3ЃЉзїжБЯпx=mНЛХзЮяЯпгкЕуPЃЌНЛЯпЖЮOBгкЕуQЃЌЕБЁїPQBЮЊЕШбќШ§НЧаЮЪБЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
вбжЊХзЮяЯпy=3ax2+2bx+c
ЃЈ1ЃЉШєa=b=1ЃЌc=-1ЧѓИУХзЮяЯпгыxжсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉШєa= ЃЌc=2+bЧвХзЮяЯпдк
ЃЌc=2+bЧвХзЮяЯпдк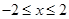 ЧјМфЩЯЕФзюаЁжЕЪЧ-3ЃЌЧѓbЕФжЕЃЛ
ЧјМфЩЯЕФзюаЁжЕЪЧ-3ЃЌЧѓbЕФжЕЃЛ
ЃЈ3ЃЉШєa+b+c=1ЃЌЪЧЗёДцдкЪЕЪ§xЃЌЪЙЕУЯргІЕФyЕФжЕЮЊ1ЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
вбжЊЙигкxвЛдЊЖўДЮЗНГЬ гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ
гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ
ЃЈ1ЃЉЧѓkШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБkзюаЁЕФећЪ§ЪБЃЌЧѓХзЮяЯп ЕФЖЅЕузјБъвдМАЫќгыxжсЕФНЛЕузјБъЃЛ
ЕФЖЅЕузјБъвдМАЫќгыxжсЕФНЛЕузјБъЃЛ
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЧѓЕУЕФХзЮяЯпдкxжсЯТЗНЕФВПЗжбиxжсЗелЕНxжсЩЯЗНЃЌЭМЯѓЕФЦфгрВПЗжВЛБфЃЌЕУЕНвЛИіаТЭМЯѓЃЎЧыФуЛГіетИіаТЭМЯѓЃЌВЂЧѓГіаТЭМЯѓгыжБЯп гаШ§ИіВЛЭЌЙЋЙВЕуЪБmжЕЃЎ
гаШ§ИіВЛЭЌЙЋЙВЕуЪБmжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКМЦЫуЬт
ШчЭМЃЌФГЙЋТЗЫэЕРКсНиУцЮЊХзЮяЯпЃЌЦфзюДѓИпЖШЮЊ6УзЃЌЕзВППэЖШOMЮЊ12Уз. ЯжвдOЕуЮЊдЕуЃЌOMЫљдкжБЯпЮЊxжсНЈСЂжБНЧзјБъЯЕ.
ЁОаЁЬт1ЁПжБНгаДГіЕуMМАХзЮяЯпЖЅЕуPЕФзјБъЃЛ
ЁОаЁЬт2ЁПЧѓетЬѕХзЮяЯпЕФНтЮіЪНЃЛ
ЁОаЁЬт3ЁПШєвЊДюНЈвЛИіОиаЮЁАжЇГХМмЁБAD- DC- CBЃЌ
ЪЙCЁЂDЕудкХзЮяЯпЩЯЃЌAЁЂBЕудкЕиУцOMЩЯЃЌ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com