在平面直角坐标系中，将抛物线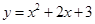
绕着它与y轴的交点旋转180°，所得抛物线的解析式为 ．
科目：初中数学 来源： 题型：填空题
某果园有100棵橘子树，平均每一棵树结600个橘子．根据经验估计，每多种一棵树，平均每棵树就会少结5个橘子．设果园增种x棵橘子树，果园橘子总个数为y个，则果园里增种 棵橘子树，橘子总个数最多．
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图，抛物线
与x轴正半轴交于点A（3，0）.以OA为边在x轴上方作正方形OABC，延长CB交抛物线于点D，再以BD为边向上作正方形BDEF，.则a= ，点E的坐标是 .
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
如图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是 .
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
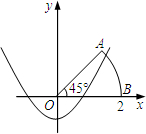
如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线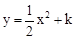
与扇形OAB的边界总有两个公共点，则实数k的取值范围是
.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，已知抛物线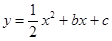
与x轴交于A，B两点，对称轴为直线
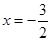，直线AD交抛物线于点D（2，3）．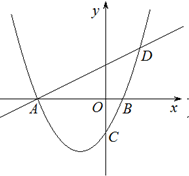
（1）求抛物线的解析式；
（2）已知点M为第三象限内抛物线上的一动点，当点M在什么位置时四边形AMCO的面积最大？并求出最大值；
（3）当四边形AMCO面积最大时，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线BC相切的圆？若存在，求出圆心Q的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（顶点式为
）．
，∴顶点坐标为（﹣1，2），当x=0时，y=3，∴与y轴的交点坐标为（0，3），∴旋转180°后的对应顶点的坐标为（1，4），∴旋转后的抛物线解析式为
，即
与抛物线
关于
轴对称,则
= ,
= 
的图像至少有三个公共点，则实数b的取值范围 .
的顶点坐标是 ．