
分析 首先求得使得一次函数y=-mx+10-m经过一、二、四象限且关于x的分式方程$\frac{mx}{x-8}$=3+$\frac{8x}{x-8}$的解为整数的数,然后直接利用概率公式求解即可求得答案.
解答 解:∵使得一次函数y=-mx+10-m经过一、二、四象限,
∴-m<0,10-m>0,
∴0<m<10,
∴符合条件的有:1,2,5,7,8,
∵mx=3(x-8)+8x,
解得:x=$\frac{24}{11-m}$,
∵x≠8,
∴11-m≠3,
∴m≠8,
∵解为整数,
∴m=5,7,-13,
∴使得一次函数y=-mx+10-m经过一、二、四象限且关于x的分式方程$\frac{mx}{x-8}$=3+$\frac{8x}{x-8}$的解为整数的有5、7,
∴使得一次函数y=-mx+10-m经过一、二、四象限且关于x的分式方程$\frac{mx}{x-8}$=3+$\frac{8x}{x-8}$的解为整数的概率是:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式的应用、一次函数的图象与系数的关系以及分式方程的解.注意根据题意求得使得一次函数y=-mx+10-m经过一、二、四象限且关于x的分式方程$\frac{mx}{x-8}$=3+$\frac{8x}{x-8}$的解为整数的数是关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
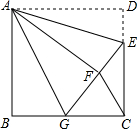 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
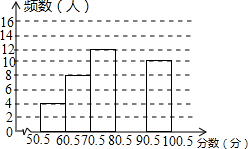 2015年11月9日是第25个全国消防日,某学校为了增强学生的安全意识,举行了一次安全知识竞赛,全校800名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中随机抽取了部分学生的成绩进行统计(满分100分,而且成绩均为整数).绘制了不完整的统计图表,请你根据图表中提供的信息解答以下问题:
2015年11月9日是第25个全国消防日,某学校为了增强学生的安全意识,举行了一次安全知识竞赛,全校800名学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中随机抽取了部分学生的成绩进行统计(满分100分,而且成绩均为整数).绘制了不完整的统计图表,请你根据图表中提供的信息解答以下问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 12 | m |
| 80.5~90.5 | n | 0.32 |
| 90.5~100.5 | 10 | 0.1 |
| 合计 | a | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com