
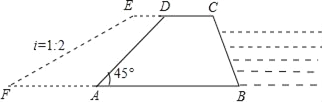
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
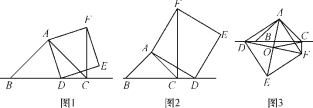
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时可以证明△ABD≌△ACF,则
①BC与CF的位置关系为: ;
②BC,DC,CF之间的数量关系为: ;
(2)类比探究
如图2,当点D在线段BC的延长线上时,其他条件不变,(1)中①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变.
①BC,DC,CF之间的数量关系为:
②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC,则OC的长度为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由点C向点D运动,设运动时间为t秒。
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,EP与PQ有什么关系?请说明理由。
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能使得△EPB与△CQP全等?此时点Q的运动速度为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】其工厂甲.乙两个部门各有员工![]() 人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取![]() 名员工进行了生产技能测试,测试成绩(百分制)如下:
名员工进行了生产技能测试,测试成绩(百分制)如下:
甲:78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙:93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
(1)按如下分数段整理、描述这两组样本数据:
成绩人数部门 |
|
|
|
|
|
|
甲 |
|
|
|
|
|
|
乙 |
(说明:成绩![]() 分及以上为生产技能优秀,
分及以上为生产技能优秀,![]() 分为生产技能良好,
分为生产技能良好,![]() 分为生产技能合格,
分为生产技能合格,![]() 分以下为生产技能不合格)
分以下为生产技能不合格)
(2)若按照甲部门的样本数据,在列频数分布表时,若取组距为![]() ,则
,则![]() 这小组的频数为 ,频率为 ;
这小组的频数为 ,频率为 ;
(3)若按照乙部门的样本数据画出扇形统计图,则表示生产技能优秀部分的圆心角是 度;
得出结论:
(4)估计乙部门生产技能优秀的员工人数为 ;
(5)可以推断出部门员工的生产技能水平较高,你的理由为 (说出一条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
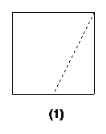
【题目】(1)如图(1),在正方形一边上取中点,并沿虚线剪开,用两块图形拼一拼,能否拼出平行四边形、梯形或三角形?画图解释你的判断.
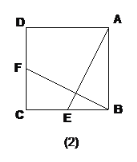
(2)如图(2)E为正方形ABCD边BC的中点,F为DC的中点,BF与AE有何关系?请解释你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,以BF为底向正方形外侧作等腰直角三角形BEF,连接DF,取DF的中点G,连接EG,CG.

(1)如图1,当点A与点F重合时,猜想EG与CG的数量关系为 ,EG与CG的位置关系为 ,请证明你的结论.
(2)如图2,当点F在AB上(不与点A重合)时,(1)中结论是否仍然成立?请说明理由;如图3,点F在AB的左侧时,(1)中的结论是否仍然成立?直接做出判断,不必说明理由.
(3)在图2中,若BC=4,BF=3,连接EC,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买8台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件100个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂买机器的预算资金不超过46万元,那么该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的8台机器生产零件的日产量不低于550个,那么为了节约资金,应该选择哪种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com