
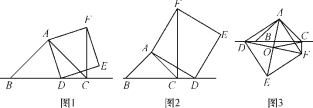
ЁОЬтФПЁПвбжЊЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌЁЯABCЃН45ЁуЃЌABЃНACЃЌЕуDЮЊжБЯпBCЩЯвЛЖЏЕу(ЕуDВЛгыBЃЌCжиКЯ)ЃЌвдADЮЊБпзїе§ЗНаЮADEFЃЌСЌНгCFЃЎ
(1)ЙлВьВТЯы
ШчЭМ1ЃЌЕБЕуDдкЯпЖЮBCЩЯЪБПЩвджЄУїЁїABDЁеЁїACFЃЌдђ
ЂйBCгыCFЕФЮЛжУЙиЯЕЮЊЃК ЃЛ
ЂкBCЃЌDCЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊЃК ЃЛ
(2)РрБШЬНОП
ШчЭМ2ЃЌЕБЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌЦфЫћЬѕМўВЛБфЃЌ(1)жаЂйЃЌЂкНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыФуаДГіе§ШЗНсТлдйИјгшжЄУїЃЛ
(3)ЭиеЙбгЩь
ШчЭМ3ЃЌЕБЕуDдкЯпЖЮBCЕФЗДЯђбгГЄЯпЩЯЪБЃЌЧвЕуAЃЌFЗжБ№дкжБЯпBCЕФСНВрЃЌЦфЫћЬѕМўВЛБфЃЎ
ЂйBCЃЌDCЃЌCFжЎМфЕФЪ§СПЙиЯЕЮЊЃК
ЂкШєе§ЗНаЮADEFЕФБпГЄЮЊ2ЃЌЖдНЧЯпAEЃЌDFЯрНЛгкЕуOЃЌСЌНгOCЃЌдђOCЕФГЄЖШЮЊ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйBCЁЭCFЃЛЂкBCЃНDCЃЋCFЃЛЃЈ2ЃЉЂйГЩСЂЃЌЂкВЛГЩСЂЃЌНсТлЂкгІИФЮЊBCЃНCFЃDCЃЌРэгЩЯъМћНтЮіЃЛЃЈ3ЃЉЂйBCЃНDCЃCFЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнSASжЄУїЁїABDЁеЁїACFЃЌПЩЕУЁЯABCЃНЁЯACFЃН45ЁуЃЌдђЁЯBCFЃНЁЯACBЃЋЁЯACFЃН90ЁуЃЌЫљвдBCЁЭCFЃЛ
ЂкгЩЁїABDЁеЁїACFЕФаджЪКЭЯпЖЮЕФКЭПЩЕУНсТлЃЛ
ЃЈ2ЃЉЂйГЩСЂЃЌжЄУїЁЯBACЃЋЁЯCADЃНЁЯDAFЃЋЁЯCADЃЌМДЁЯBADЃНЁЯCAFЃЌЭЌРэжЄУїЁїABDЁеЁїACFЃЌПЩЕУBCЁЭCFЃЌ
ЂкВЛГЩСЂЃЌгЩBDЃНBCЃЋCDЃЌBDЃНCFЃЌПЩЕУаТЕФНсТлЃКBCЃНCFDCЃЛ
ЃЈ3ЃЉЂйИљОнЭМ3жЊЃКDCзюГЄЃЌЭЌРэЃКЁїDABЁеЁїFACЃЌдђBDЃНCFЃЌПЩЕУBCЃНDCCFЃЛ
ЂкЯШИљОне§ЗНаЮЕФБпГЄЧѓЖдНЧЯпDFЕФГЄЃЌжЄУїЁЯDCFЃН90ЁуЃЌИљОнжБНЧШ§НЧаЮаББпжаЯпЕФаджЪПЩЕУOCЕФГЄЃЎ
ЃЈ1ЃЉЂйBCЁЭCFЃЌРэгЩЪЧЃК
ШчЭМ1ЃЌЁпЫФБпаЮADEFЪЧе§ЗНаЮЃЌ
ЁрЁЯDAFЃН90ЁуЃЌADЃНAFЃЌ
ЁпЁЯBACЃН90ЁуЃЌ
ЁрЁЯBADЃЋЁЯDACЃНЁЯDACЃЋЁЯCAFЃЌ
ЁрЁЯBADЃНЁЯCAFЃЌ
дкЁїBADКЭЁїCAFжаЃЌ
Ёп ЃЌ
ЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌ
ЁрЁЯABCЃНЁЯACFЃН45ЁуЃЌ
ЁпЁЯACBЃН45ЁуЃЌ
ЁрЁЯBCFЃНЁЯACBЃЋЁЯACFЃН90ЁуЃЌ
ЁрBCЁЭCFЃЛ
ЂкBCЃНDCЃЋCFЃЌ
РэгЩЪЧЃКгЩЂйжЊЃКЁїABDЁеЁїACFЃЌ
ЁрBDЃНCFЃЌ
ЁрBCЃНBDЃЋCDЃНCFЃЋCDЃЛ
ЙЪД№АИЮЊЃКЂйBCЁЭCFЃЌЂкBCЃНCFЃЋCDЃЛ
ЃЈ2ЃЉЂйГЩСЂЃЌЂкВЛГЩСЂЃЌНсТлЂкгІИФЮЊBCЃНCFDCЃЛ
жЄУїЃКШчЭМ2ЃЌдке§ЗНаЮADEFжаЃЌ
ADЃНAFЃЌЁЯDAFЃН90ЁуЃЌ
ЁпЁЯBACЃН90ЁуЃЌ
ЁрЁЯBACЃЋЁЯCADЃНЁЯDAFЃЋЁЯCADЃЌМДЁЯBADЃНЁЯCAFЃЌ
ЁпЁЯABCЃН45ЁуЃЌ
ЁрЁЯACBЃН180ЁуЁЯBACЁЯABCЃН45ЁуЃЌ
ЁрЁЯABCЃНЁЯACBЃЌ
ЁрABЃНACЃЌ
дкЁїABDгыЁїACFжаЃЌ ЃЌ
ЃЌ
ЁрЁїABDЁеЁїACFЃЌ
ЁрЁЯACFЃНЁЯABDЃН45ЁуЃЌBDЃНCFЃЌ
ЁпЁЯACBЃН45ЁуЃЌ
ЁрЁЯBCFЃНЁЯACBЃЋЁЯACFЃН90ЁуЃЌ
ЁрBCЁЭCFЃЛ
ЁпBDЃНBCЃЋCDЃЌBDЃНCFЃЌ
ЁрBCЃНCFDCЃЛ
ЃЈ3ЃЉЂйBCЃНDCCFЃЌ
РэгЩЪЧЃКШчЭМ3ЃЌЭЌРэЕУЃКЁЯDABЃНЁЯFACЃЌ
взжЄЕУЃКЁїDABЁеЁїFACЃЌ
ЁрBDЃНCFЃЌ
ЁрDCЃНBDЃЋBCЃНCFЃЋBCЃЌ
ЁрBCЃНDCCFЃЛ
Ђке§ЗНаЮADEFжаЃЌБпГЄEFЃН2
ЁрDFЃН2![]()
ЁпЁЯABCЃН45Ёу
ЁрЁЯABDЃН135Ёу
ЁпЁїDABЁеЁїFAC
ЁрЁЯACFЃНЁЯABDЃН135Ёу
ЁпЁЯACBЃН45Ёу
ЁрЁЯDCFЃН90Ёу
ЁпЫФБпаЮADEFЪЧе§ЗНаЮ
ЁрODЃНOF
ЁрOCЃН![]() DFЃН
DFЃН![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃКЂйBCЃНDCCFЃЌЂк![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫФБпаЮABCDКЭЫФБпаЮOEFGЖМЪЧе§ЗНаЮЃЌЕуOЪЧе§ЗНаЮABCDСНЖдНЧЯпЕФНЛЕуЃЌвбжЊABЃН2ЃЌEFЃН3ЃЌе§ЗНаЮOEFGШЦЕуOзЊЖЏЃЌOEНЛBCЩЯвЛЕуNЃЌOGНЛCDЩЯвЛЕуM.ЧѓЫФБпаЮOMCNЕФУцЛ§ЃЎ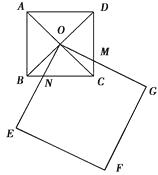
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЯдЪОСЫгУМЦЫуЛњФЃФтЫцЛњЭЖжРвЛУЖЭМЖЄЕФФГДЮЪЕбщЕФНсЙћЃЎ

ЯТУцгаШ§ИіЭЦЖЯЃК
ЂйЕБЭЖжРДЮЪ§ЪЧ500ЪБЃЌМЦЫуЛњМЧТМЁАЖЄМтЯђЩЯЁБЕФДЮЪ§ЪЧ308ЃЌЫљвдЁАЖЄМтЯђЩЯЁБЕФИХТЪЪЧ0.616ЃЛ
ЂкЫцзХЪЕбщДЮЪ§ЕФдіМгЃЌЁАЖЄМтЯђЩЯЁБЕФЦЕТЪзмдк0.618ИННќАкЖЏЃЌЯдЪОГівЛЖЈЕФЮШЖЈадЃЌПЩвдЙРМЦЁАЖЄМтЯђЩЯЁБЕФИХТЪЪЧ0.618ЃЛ
ЂлШєдйДЮгУМЦЫуЛњФЃФтЪЕбщЃЌдђЕБЭЖжРДЮЪ§ЮЊ1000ЪБЃЌЁАЖЄМтЯђЩЯЁБЕФИХТЪвЛЖЈЪЧ0.620ЃЎ
ЦфжаКЯРэЕФЪЧЃЈ ЃЉ
A. Ђй B. Ђк C. ЂйЂк D. ЂйЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
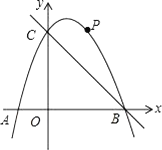
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§y=Љx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌ3ЃЉЃЌAЕудкдЕуЕФзѓВрЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎЕуPЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЧвдкжБЯпBCЕФЩЯЗНЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЎ
ЃЈ2ЃЉСЌНгPOЁЂPCЃЌВЂАбЁїPOCбиCOЗелЃЌЕУЕНЫФБпаЮPOPЁфCЃЌФЧУДЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮ ABPCЕФУцЛ§зюДѓЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъКЭЫФБпаЮABPCЕФзюДѓУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2Ѓ6xЃЋaЃ2ЃН0ЃЎ
ЃЈ1ЃЉШчЙћИУЗНГЬгаЪЕЪ§ИљЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШчЙћИУЗНГЬгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЧѓГіетСНИіИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖЙВ500УћбЇЩњВЮМгЗЈТЩжЊЪЖВтЪдЃЌДгжаЫцЛњГщШЁвЛВПЗжЪдОэГЩМЈЃЈЕУЗжШЁећЪ§ЃЉЮЊбљБОзїЭГМЦЗжЮіЃЌНјааећРэКѓЗжГЩЮхзщЃЌВЂЛцжЦГЩЦЕЪ§ЗжВМжБЗНЭМ(МћЭМ)ЧыНсКЯжБЗНЭМЬсЙЉЕФаХЯЂЃЌНтД№вдЯТЮЪЬтЃК

ЃЈ1ЃЉЫцЛњГщШЁСЫЖрЩйУћбЇЩњЕФВтЪдГЩМЈЃП
ЃЈ2ЃЉ70.5ЁЋ80.5етвЛЗжЪ§ЖЮЕФЦЕТЪЪЧЖрЩйЃП
ЃЈ3ЃЉШє90ЗжвдЩЯЃЈВЛКЌ90ЗжЃЉЖЈЮЊгХауЃЌбљБОжаЕФгХауТЪЪЧЖрЩйЃП
ЃЈ4ЃЉЧыЙРМЦГіИУаЃОХФъМЖетДЮЗЈТЩжЊЪЖВтЪдЛёЕУгХауЕФДѓдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌFЮЊЯвACЕФжаЕуЃЌСЌНгOFВЂбгГЄНЛ![]() гкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпЃЌНЛBAЕФбгГЄЯпгкЕуEЃЎ
гкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпЃЌНЛBAЕФбгГЄЯпгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКACЁЮDEЃЛ
ЃЈ2ЃЉСЌНгCDЃЌШєOA=AE=1ЃЌЧѓЫФБпаЮACDEУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭъГЩЯТУцЭЦРэЙ§ГЬЃК
ШчЭМЃЌвбжЊЁЯB+ЁЯBCD=180ЁуЃЌЁЯB=ЁЯDЃЎЧѓжЄЃКЁЯE=ЁЯDFEЃЎ
жЄУїЃКЁпЁЯB+ЁЯBCD=180ЁуЃЌ
ЁрABЁЮ ( )
ЁрЁЯB=ЁЯDCE( )
гжЁпЁЯB=ЁЯDЃЌ
ЁрЁЯDCE=ЁЯD( )
Ёр ЁЮ ( )
ЁрЁЯE=ЁЯDFE( )

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
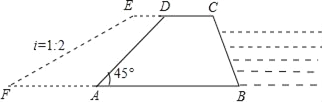
ЁОЬтФПЁПШчЭМЃЌЙуАВЪаЗРКщжИЛгВПЗЂЯжЧўНБпвЛДІГЄ400УзЃЌИп8УзЃЌБГЫЎЦТЕФЦТНЧЮЊ45ЁуЕФЗРКщДѓЕЬЃЈКсНиУцЮЊЬнаЮABCDЃЉМБашМгЙЬЃЎОЕїВщТлжЄЃЌЗРКщжИЛгВПзЈМвзщжЦЖЈЕФМгЙЬЗНАИЪЧЃКБГЫЎЦТУцгУЭСЪЏНјааМгЙЬЃЌВЂЪЙЩЯЕзМгПэ2УзЃЌМгЙЬКѓЃЌБГЫЎЦТEFЕФЦТБШi=1ЃК2ЃЎ
ЃЈ1ЃЉЧѓМгЙЬКѓАгЕздіМгЕФПэЖШAFЕФГЄЃЛ
ЃЈ2ЃЉЧѓЭъГЩетЯюЙЄГЬашвЊЭСЪЏЖрЩйСЂЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com