
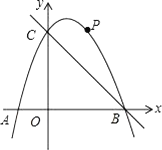
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
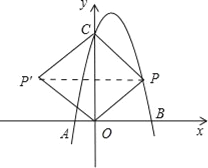
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形ABPC的最大面积.
【答案】(1)二次函数的表达式为y=﹣x2+2x+3;(2)存在点P,使四边形POP′C为菱形,P点的坐标为(![]() ,
, ![]() );(3)P点的坐标为(
);(3)P点的坐标为(![]() ,
, ![]() ),四边形ABPC面积的最大值为
),四边形ABPC面积的最大值为![]() .
.
【解析】试题分析:(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相平分,可得P点的纵坐标,根据函数值与自变量的对应关系,可得答案;
(3)根据面积的和差,可得二次函数,根据二次函数的性质,可得m的值,根据自变量与函数值的对应关系,可得P点坐标.
试题解析:(1)将B、C两点的坐标代入得![]() ,解得
,解得![]() ,
,
所以二次函数的表达式为y=﹣x2+2x+3;
(2)如图,存在点P,使四边形POP′C为菱形.
设P点坐标为(x,﹣x2+2x+3),PP′交CO于E,
若四边形POPC是菱形,则有PC=PO,
连接PP则PE⊥CO于E,
∴OE=CE=![]() ,
,
∴y=![]() ,
,
∴-x2+2x+3=![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (不合题意,舍去),
(不合题意,舍去),
∴P点的坐标为(![]() ,
, ![]() );
);
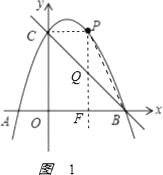
(3)如图1,
 ,
,
过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,﹣x2+2x+3)
易得,直线BC的解析式为y=﹣x+3.
则Q点的坐标为(x,﹣x+3).
PQ=﹣x2+3x.
S四边形ABPC=S△ABC+S△BPQ+S△CPQ=![]() ABOC+
ABOC+![]() QPBF+
QPBF+![]() QPOF=
QPOF=![]() ×4×3+
×4×3+![]() (﹣x2+3x)×3=﹣
(﹣x2+3x)×3=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
当x=![]() 时,四边形ABPC的面积最大,
时,四边形ABPC的面积最大,
此时P点的坐标为(![]() ,
, ![]() ),四边形ABPC面积的最大值为
),四边形ABPC面积的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的有( ).①对顶角相等;②过直线外一点有且只有一条直线与已知直线平行;③同旁内角互补;④在同一平面内,垂直于同一条直线的两条直线平行
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
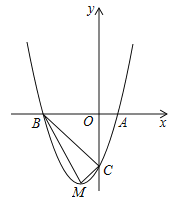
【题目】如图,顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举办一项小制作评比活动,对初一年级6个班的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1,其中三班的件数是8.

请你回答:
(1)本次活动共有 件作品参赛;
(2)经评比,四班和六班分别有10件和2件作品获奖,那么你认为这两个班中哪个班获奖率较高?为什么?
(3)小制作评比结束后,组委会评出了4件优秀作品A、B、C、D.现决定从这4件作品中随机选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B、D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.

(1)写出y与t之间的函数关系式.
(2)通话2分钟应付通话费多少元?
(3)通话7分钟呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月1日,小明将一笔钱存入银行,定期3年,年利率是5%,若到期后取出,他可得本息和为23000元,则小明存入的本金是_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2﹣4ac>0;(2)c>1;(3)2a﹣b<0;(4)a+b+c<0,其中错误的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com