
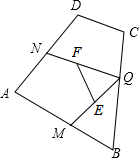
 如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.
如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.  智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
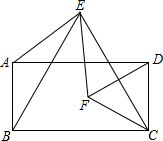 已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.
已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
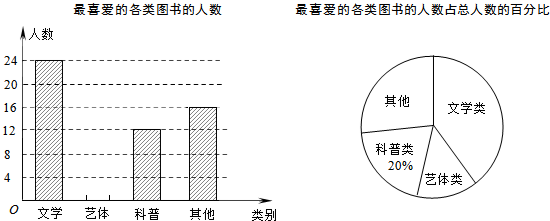
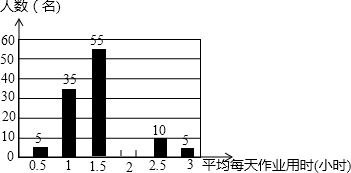 为切实减轻学生课业负担,学校教务处调查了本校学生平均每天完成作业所用时间的情况,随机调查了150名同学,下图是根据调查所得数据绘制的不完整的统计图
为切实减轻学生课业负担,学校教务处调查了本校学生平均每天完成作业所用时间的情况,随机调查了150名同学,下图是根据调查所得数据绘制的不完整的统计图| 平均每天作业用时t(小时) | 作业量 |
| t<1 | 较轻 |
| 1≤t≤2 | 合适 |
| t>2 | 较重 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
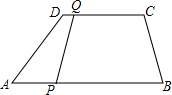 如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.
如图,在梯形ABCD中,CD∥AB,且CD=6cm,AB=9cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向B运动,Q以2cm/s的速度由C向D运动.则2或3秒时,直线QP将四边形ABCD截出一个平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com