
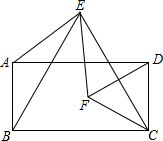
 已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.
已知:如图所示,四边形ABCD是矩形,分别以BC、CD为一边作等边△EBC和等边△FCD,点E在矩形上方,点F在矩形内部,连接AE、EF.分析 (1)由矩形的性质得出∠BCD=90°,由等边三角形的性质得出∠ECD=30°,得出∠ECF=30°;
(2)由SAS证明△EBA≌△ECF,得出对应边相等即可.
解答 (1)解:∵四边形ABCD是矩形,
∴∠BCD=∠ABC=90°,AB=CD,
∵三角形△EBC是等边三角形,
∴∠ECB=∠EBC=60°,EC=EB,
∴∠ECD=∠BCD-∠ECB=90°-60°=30°,∠EBA=90°-60°=30°,
∵△FCD是等边三角形,
∴∠FCD=60°,CF=CD,
∴∠ECF=∠FCD-∠ECD=30°;
(2)证明:∵AB=CD,CF=CD,
∴AB=CF,
在△EBA和△ECF中,
$\left\{\begin{array}{l}{AB=CF}&{\;}\\{∠EBA=∠ECF=30°}&{\;}\\{EB=EC}&{\;}\end{array}\right.$,
∴△EBA≌△ECF(SAS),
∴AE=FE.
点评 本题考查了矩形的性质、等边三角形的性质、全等三角形的判定与性质;熟练掌握矩形和等边三角形的性质,并能进行推理论证与计算是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (1+a)(a+1) | B. | ($\frac{1}{2}$x+y)(-y+$\frac{1}{2}$x) | C. | (x2-y)(x+y2) | D. | (x-y)(-x+y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
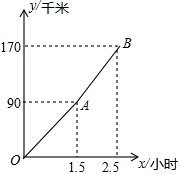 “五一节”期间,小华一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.下列结论:
“五一节”期间,小华一家自驾游去了离家170千米的某地,如图是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.下列结论:| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
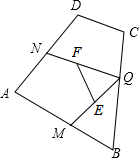 如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.
如图,四边形ABCD中,∠A=90°、AM=4、AN=3,一动点Q沿着M→B→C→D→N的路径运动(不与点M、N重合);点E、F分别为线段MQ、NQ的中点,则线段EF的长度为$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
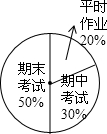 某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( )
某初中一个学期的数学总平均分是按扇形图信息要求进行计算的,该校胡军同学这个学期的数学成绩如下:则胡军这个学期数学总平均分为( ) | 胡军 | 平时作业 | 期中考试 | 期末考试 |
| 90 | 85 | 88 |
| A. | 87.5 | B. | 87.6 | C. | 87.7 | D. | 87.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
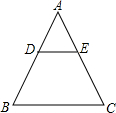 如图,在△ABC在,DE∥BC,$\frac{AD}{DB}$=$\frac{2}{3}$,S△ADE=8,则四边形BDEC的面积为42.
如图,在△ABC在,DE∥BC,$\frac{AD}{DB}$=$\frac{2}{3}$,S△ADE=8,则四边形BDEC的面积为42.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com