
����Ŀ��ij��װ������һ�ּп˺�T�����п�ÿ������100Ԫ��T��ÿ������60Ԫ�������ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ�����
�� ��һ���п���һ��T����
�� �п˺�T���������۵�80%���
��ij�ͻ�Ҫ���÷�װ������п�30����T��x����x >30����
��1�����ÿͻ��������ٹ��п��踶��______Ԫ��T���踶��______Ԫ���ú�x��ʽ�ӱ�ʾ����
���ÿͻ��������ڹ��п��踶��______Ԫ��T���踶��______Ԫ���ú�x��ʽ�ӱ�ʾ����
��2����x=40��ͨ������˵���������١����������ַ��������Ϊ���㣿
��3���������Żݷ�����ͬʱʹ�ã���x=40ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������˵�����ɣ�
���𰸡�(1)3000�� ![]() ��2400��
��2400�� ![]() ����2��������1������3�����÷�����1����30���п˻���30��T�������÷�����2����10��T������ʱ������ʡ.
����2��������1������3�����÷�����1����30���п˻���30��T�������÷�����2����10��T������ʱ������ʡ.
�����������������������������ķ����г�ʽ�Ӽ���
���������
��1�������٣��п˵ķ��ã�30��100=3000Ԫ��T���ķ���Ϊ��60��x-30��Ԫ��
�����ڣ��п˵ķ��ã�30��100��0.8=2400Ԫ��T���ķ���Ϊ��60��0.8x=48xԪ��
��2����x=40ʱ��
������3000+60��40-30��=3600Ԫ
������2400+48��40=4320Ԫ
��Ϊ3600��4320�����������ٺ��㣮
��3������30�пˣ���ʱT������30����
ʣ�µ�10����T���÷����ڹ���ʱ10����T������Ϊ��10��60��0.8=480��
���ʱ�������ˣ�3000+480=3480��3600
������������30�п˺�T�����ٰ���������10���п˺�T����ʡǮ��
�ʴ�Ϊ����1��3000��60��x-30����2400��48x��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�Լ��ˮ��ij�о�������������ˮ�շѷ������涨���ÿ��ÿ����ˮ������10�֣�ÿ��ˮ�շ�2Ԫ�����ÿ��ÿ����ˮ����10�֣�����������ÿ��ˮ�շ�2.5Ԫ��С�쿴�������շѷ���������������ÿ�µ�ˮ����
��1�����С���ÿ����ˮ8�֣���ˮ���� Ԫ�����С���ÿ����ˮ20�֣���ˮ���� Ԫ��
��2�������ĸ![]() ��ʾС���ÿ����ˮ�Ķ�������ôС���ÿ�µ�ˮ�Ѹ������
��ʾС���ÿ����ˮ�Ķ�������ôС���ÿ�µ�ˮ�Ѹ������![]() �Ĵ���ʽ��ʾ�أ�
�Ĵ���ʽ��ʾ�أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
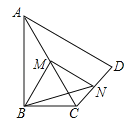
����Ŀ����ͼ�����ı���ABCD�У���ABC=90����AC=AD��M��N�ֱ�ΪAC��AD���е㣬����BM��MN��BN��
��1����֤��BM=MN��
��2����BAD=60����ACƽ����BAD��AC=2����BN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��P��B��C��Բ�ϵ��ĸ��㣬��APC=��CPB=60�㣬AP��CB���ӳ����ཻ�ڵ�D��
��1����֤����ABC�ǵȱ������Σ�
��2������PAC=90�㣬AB=![]() ����PD�ij���
����PD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ�ˡ�����֪ʶ������������һ����Ϊ���С�飬�涨���һ���50�֣����һ���10�֣������ʱ���Ƿ�Ա�����˸���С�������÷����£�
1�� | 2�� | 3�� | 4�� | 5�� |
100 | 150 | ��400 | 350 | ��100 |
��1����һ�������ڶ������ٷ֣�
��2����һ���������������ٷ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����д�����ǣ�������

A. ��AB=BCʱ���������� B. ��AC��BDʱ����������
C. ��AC=BDʱ�����Ǿ��� D. ����ABC=90��ʱ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y������x+h��2����x����3ʱ��y��x�����������x����3ʱ��y��x���������С����x��0ʱ��y��ֵΪ�� ��
A. ��1B. ��9C. 1D. 9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD����PΪ�Խ���AC��һ�����㣬QΪCD����һ�㣬��![]()
��1����֤��PB=PQ��
��2����BC+CQ=8�����ı���VCQP�������
��3����AP=x��ABCD�����Ϊy����CQ=2����y��x�ĺ�����ϵʽ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
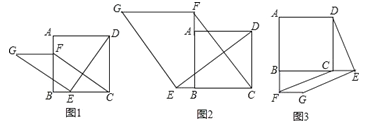
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� ��λ�ù�ϵ�� ��
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������ж���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com