
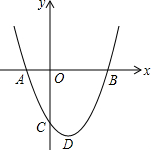
 如图,抛物线y=x2+bx+c交x轴于点A(-1,0)和点B(m,0),交y轴于点C,抛物线的顶点为D,m>1.
如图,抛物线y=x2+bx+c交x轴于点A(-1,0)和点B(m,0),交y轴于点C,抛物线的顶点为D,m>1.分析 (1)根据抛物线与x轴的交点坐标列出解析式,与已知解析式比较,表示出b与c即可;
(2)把抛物线解析式表示为顶点形式,表示出D坐标即可;
(3)连接AD,BD,过D作DE垂直于x轴,利用等边三角形的性质得到DE=$\sqrt{3}$AE,即可确定出m的值.
解答 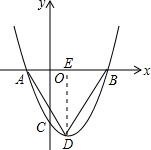 解:(1)∵抛物线y=x2+bx+c交x轴于点A(-1,0)和点B(m,0),
解:(1)∵抛物线y=x2+bx+c交x轴于点A(-1,0)和点B(m,0),
∴x2+bx+c=(x+1)(x-m)=x2-(m-1)x-m,
则b=1-m,c=-m;
(2)y=x2+(1-m)x-m=(x+$\frac{1-m}{2}$)2-$\frac{(m+1)^{2}}{4}$,
则顶点D的坐标为(-$\frac{1-m}{2}$,-$\frac{(m+1)^{2}}{4}$);
(3)若△ABD为等边三角形,作DE⊥x轴,
可得DE=$\sqrt{3}$AE,
∵DE=$\frac{(m+1)^{2}}{4}$,AE=1-$\frac{1-m}{2}$=$\frac{m+1}{2}$,
∴$\frac{m+1}{2}$=$\sqrt{3}$,
解得:m=2$\sqrt{3}$-1.
点评 此题考查了抛物线与x轴的交点,熟练掌握二次函数的性质是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | sin35°+sin45°=sin80° | B. | cos30°+cos15°=cos45° | ||
| C. | tan60°+cos22°=tan82° | D. | tan30°=$\frac{sin30°}{cos30°}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
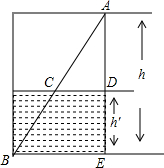 如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.
如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
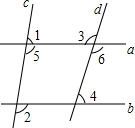 如图,∠1+∠2=180°,∠3=108°,求∠4的度数的过程填写完整.
如图,∠1+∠2=180°,∠3=108°,求∠4的度数的过程填写完整.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
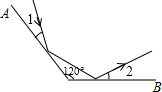 如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )
如图,平面镜A与B之间的夹角为120°,光线经平面镜A反射后射在平面镜B上,再反射出去,若∠1=∠2,则∠1的度( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com