
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
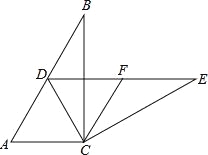
【答案】(1)、n=60;(2)、菱形;证明过程见解析
【解析】
试题分析:(1)、利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;
(2)、利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.
试题解析:(1)、∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC, ∴AC=DC,∠A=60°, ∴△ADC是等边三角形, ∴∠ACD=60°, ∴n的值是60;
(2)、四边形ACFD是菱形; 理由:∵∠DCE=∠ACB=90°,F是DE的中点, ∴FC=DF=FE,
∵∠CDF=∠A=60°, ∴△DFC是等边三角形, ∴DF=DC=FC, ∵△ADC是等边三角形,
∴AD=AC=DC, ∴AD=AC=FC=DF, ∴四边形ACFD是菱形.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】一天时间为86400秒,用科学记数法表示这一数字是( )
A.864×102
B.86.4×103
C.8.64×104
D.0.864×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,在长方形OABC中,点A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,求所有满足条件的点P的坐标.
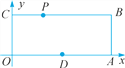
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数 | 中位数 | 众数 | 方差 |
8.5 | 8.3 | 8.1 | 0.15 |
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
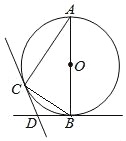
【题目】如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC.
(1)求∠A的度数;
(2)若点D到BC的距离为2,那么⊙O的半径是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.下列三个条件:①AB∥CD,②∠B=∠C.③∠E=∠F.从中任选两个作为条件,另一个作为结论,编一道数学题,并说明理由.
已知: ;
结论: ;
理由: 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com