
某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的 总费用不超过2000元,那么最多可购买多少个甲礼品?
总费用不超过2000元,那么最多可购买多少个甲礼品?
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
下列说法正确的是( )
A. 了解飞行员视力的达标率应使用抽样调查
B. 一组数据3,6,6,7,9的中位数是6
C. 从2000名学生中选200名学生进行抽样调查,样本容量为2000
D. 掷一枚质地均匀的硬币,正面朝上是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
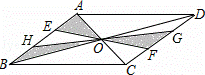
如图,▱ABCD的对角线AC、BD相交于点O,EF、GH过点O,且点E、H在边AB上,点G、F在边CD上,向▱ABCD内部投掷飞镖(每次均落在▱ABCD内,且落在▱ABCD 内任何一点的机会均等)恰好落在阴影区域的概率为( )
内任何一点的机会均等)恰好落在阴影区域的概率为( )
A.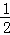 B.
B. 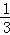 C.
C. 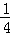 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在A处看建筑物CD的顶端D的仰角为α,且tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为 米.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
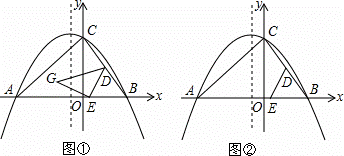
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
A. 掷一枚硬币,正面一定朝上
B. 某种彩票中奖概率为1%,是指买100张彩票一定有1张中奖
C. 旅客上飞机前的安检应采用抽样调查
D. 方差越大,数据的波动越大
查看答案和解析>>
科目:初中数学 来源: 题型:
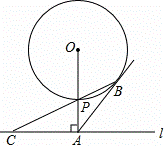
如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若PC=2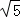 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
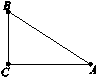
已知A,B,C三地位置如图5所示,∠C=90°,A,C两地的距离是4 km,
B,C两地的距离是3 km,则A,B两地的距离是 km;若A地在
C地的正东方向,则B地在C地的 方向.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com