
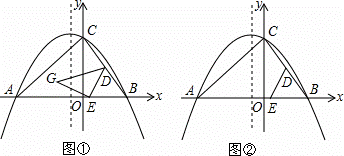
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为y=ax2+bx+8.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线y=ax2+bx+8的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
解:(1)∵抛物线y=ax2+bx+8经过点A(﹣6,0),B(4,0),
∴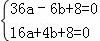
解得
∴抛物线的解析式是:y=﹣ x2﹣
x2﹣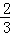 x+8.
x+8.
(2)如图①,作DM⊥抛物线的对称轴于点M, ,
,
设G点的坐标为(﹣1,n),
由翻折的性质,可得BD=DG,
∵B(4,0),C(0,8),点D为BC的中点,
∴点D的坐标是(2,4),
∴点M的坐标是(﹣1,4),DM=2﹣(﹣1)=3,
∵B(4,0),C(0,8),
∴BC=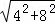 =4
=4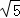 ,
,
∴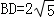 ,
,
在Rt△GDM中,
32+(4﹣n)2=20,
解得n=4± ,
,
∴G点的坐标为(﹣1,4+ )或(﹣1,4﹣
)或(﹣1,4﹣ ).
).
(3)抛物线y=ax2+bx+8的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形.
①当CD∥EF,且点E在x轴的正半轴时,如图②,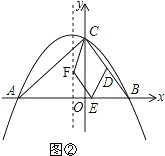 ,
,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(﹣1,d),
则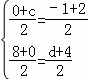
解得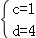
∴点F的坐标是(﹣1,4),点C的坐标是(1,0).
②当CD∥EF,且点E在x轴的负半轴时,如图③,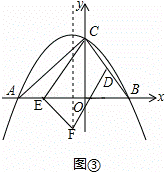 ,
,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(﹣1,d),
则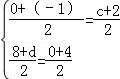
解得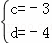
∴点F的坐标是(﹣1,﹣4),点C的坐标是(﹣3,0).
③当CE∥DF时,如图④,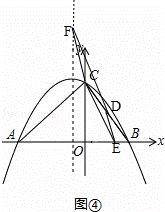 ,
,
由(2),可得点D的坐标是(2,4),
设点E的坐标是(c,0),点F的坐标是(﹣1,d),
则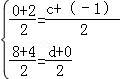
解得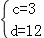
∴点F的坐标是(﹣1,12),点C的坐标是(3,0).
综上,可得
抛物线y=ax2+bx+8的对称轴上存在点F,使得以C、D、E、F为顶点的四边形为平行四边形,
点F的坐标是(﹣1,4)、(﹣1,﹣4)或(﹣1,12).


科目:初中数学 来源: 题型:
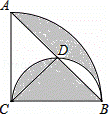
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆交AB于点D,连接CD,则阴影部分的面积是( )
A.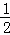 π﹣1 B.
π﹣1 B. 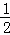 π﹣2 C. π﹣2 D. π﹣1
π﹣2 C. π﹣2 D. π﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
(1)判断DE与⊙O的位置关系并说明理由;
(2)若AC=16,tanA=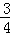 ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的 总费用不超过2000元,那么最多可购买多少个甲礼品?
总费用不超过2000元,那么最多可购买多少个甲礼品?
查看答案和解析>>
科目:初中数学 来源: 题型:
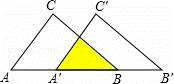
如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB=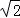 ,则此三角形移动的距离AA′是( )
,则此三角形移动的距离AA′是( )
A. 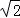 ﹣1 B.
﹣1 B. 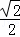 C. 1 D.
C. 1 D. 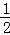
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com