
【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.

【答案】(2![]() +2,4)或(12,4).
+2,4)或(12,4).
【解析】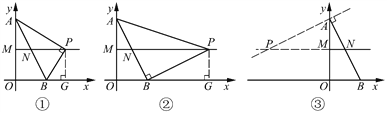
如图,∠APB=90°,∠ABP=90°,∠BAP=90°均可以使△ABP是直角三角形,故本题应该对这三种情况分别进行讨论.
(1) ∠APB=90°,如图①.
过点P作PG⊥OB,垂足为G.
∵点A的坐标为(0, 8),点B的坐标为(4, 0),
∴OA=8,OB=4.
∴在Rt△AOB中, ![]() .
.
∵点M,N分别是OA,AB的中点,
∴MN∥OB, ![]() ,
, ![]() .
.
∵MN∥OB,PG⊥OB,
∴PG=OM=4.
设PN=x,则MP=MN+PN=2+x,
∵OG=MP=2+x,
∴BG=OG-OB=2+x-4=x-2.
∵在Rt△AMP中,AP2=AM2+PM2=42+(2+x)2=16+(2+x)2,
在Rt△BGP中,BP2=BG2+PG2=(x-2)2+42=(x-2)2+16,
又∵在Rt△APB中,AB2=AP2+BP2,
∴16+(2+x)2+(x-2)2+16=![]() =80.
=80.
∴x=![]() ,即PN=
,即PN=![]() .
.
∵OG=2+x=![]() ,PG =4.
,PG =4.
∴点P的坐标为(![]() , 4).
, 4).
(2) ∠ABP=90°,如图②.
过点P作PG⊥OB,垂足为G.
设PN=x,则MP=OG=2+x,BG=x-2.
∵![]() ,AM=4,PG=4,
,AM=4,PG=4,
又∵在Rt△AMP中,AP2=16+(2+x)2,
在Rt△BGP中,BP2=(x-2)2+16,
∴在Rt△APB中,AB2=AP2-BP2=16+(2+x)2-[(x-2)2+16]= ![]() =80.
=80.
∴x=10即PN=10.
∵OG=2+x=2+10=12,PG=4.
∴点P的坐标为(12, 4).
(3) ∠BAP=90°,如图③.
由图③可以看出,在此种情况下点P不在射线MN上,不符合题意.
综上所述,点P的坐标为(![]() , 4)或(12, 4).
, 4)或(12, 4).
故本题应填写:(![]() , 4)或(12, 4).
, 4)或(12, 4).


科目:初中数学 来源: 题型:
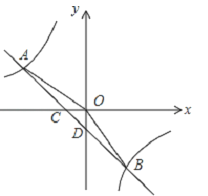
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
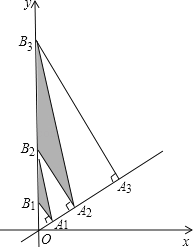
【题目】如图,直线y=![]() x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=
x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n分别过点A1,A2,A3,…An+1作直线y=![]() x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为________.(用含有正整数n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y=![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).

(1)观察每次变换前后的三角形有何变化,找出规律,按些变换规律将△OA3B3变换成△OA4B4,则A4的坐标是_______,B4的坐标是_________.
(2)若按第(1)题的规律将△OAB进行了n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测An的坐标是_______,Bn的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(2x,3x-1)是平面直角坐标系上的点。
(1)若点P在第一象限的角平分线上,求x的值;
(2)若点P在第三象限,且到两坐标轴的距离之和为16,求x的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com