
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,
,![]() ,且
,且![]() .
.
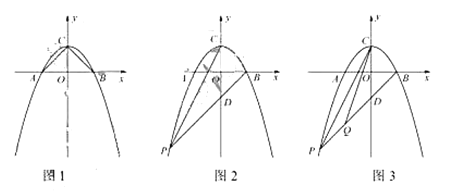
(1)如图,求![]() 、
、![]() 的值;
的值;
(2)如图,点![]() 在第三象限的抛物线上,
在第三象限的抛物线上,![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)如图,在(2)的条件下,点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,c=2(2)d=-t(t<-2);(3)
,c=2(2)d=-t(t<-2);(3) ![]()
【解析】
(1)根据三角形的面积公式求出B、C两点坐标,代入抛物线解析式,解方程组即可解决问题.
(2)设直线PB解析式为y=kx+b,把![]() ,B(2,0)代入,解方程组即可.
,B(2,0)代入,解方程组即可.
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 在抛物线上,连接
在抛物线上,连接![]() ,证明
,证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,
,![]() ,根据
,根据![]() ,得到
,得到![]() ,则
,则![]() 又
又![]() ,得到
,得到![]() ,则
,则![]() ,
,![]() ,即可求出
,即可求出![]() 的值,即可求解.
的值,即可求解.
(1)抛物线![]() 的对称轴为
的对称轴为![]() 轴,
轴,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
(2)![]() ,∵
,∵![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() .
.
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 在抛物线上,连接
在抛物线上,连接![]() ,
,
则![]() ,
,![]() ,∴
,∴![]() ,
,
过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
设![]() ,则
,则![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
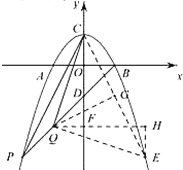
【题目】如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=![]() ,求AB的长;
,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=![]() AF.
AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
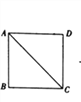
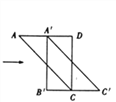
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△![]() ,当两个三角形重叠的面积为32时,则它移动的距离
,当两个三角形重叠的面积为32时,则它移动的距离![]() 等于_____.
等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将连续的奇数1,3,5,7…按如图中的方式排成一个数,用一个十字框框住5个数,这样框出的任意5个数中,四个分支上的数分别用a,b,c,d表示,如图所示.

(1)计算:若十字框的中间数为17,则a+b+c+d=______.
(2)发现:移动十字框,比较a+b+c+d与中间的数.猜想:十字框中a、b、c、d的和是中间的数的______;
(3)验证:设中间的数为x,写出a、b、c、d的和,验证猜想的正确性;
(4)应用:设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).
(1)画出△ABC关于原点O成中心对称的图形△A1B1C1;
(2)在(1)的条件下直接写出点A1的坐标为______;B1的坐标为______;
(3)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
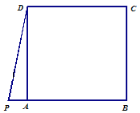
【题目】如图,正方形 ABCD 中,P 是 BA 延长线上一点,且PDA (0 45).点 A,点 E 关于 DP 对称,连接 ED,EP ,并延长 EP 交射线CB 于点 F ,连接 DF .
(1)请按照题目要求补全图形.
(2)求证:∠EDF=∠CDF
(3)求∠EDF(含有 的式子表示);
(4)过 P 做PH⊥DP交 DF 于点 H ,连接 BH , 猜想 AP 与 BH 的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com