练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．先化简，再求值：（$\frac{{a}^{2}+1}{a}$-2）÷$\frac{（a+2）（a-1）}{{a}^{2}+2a}$，其中a2-4=0．

    分析 先算括号里面的，再算除法，最后求出a的值代入进行计算即可．

    解答 解：原式=$\frac{{a}^{2}+1-2a}{a}$•$\frac{a}{a-1}$=$\frac{（a-1）^{2}}{a-1}$=a-1，
    解方程a2-4=0得，a=2或a=-2，
    当a=-2时，a2+2a=0，无意义；
    当a=2时，原式=2-1=1．

    点评 本题考查的是分式的化简求值，此类题型的特点是：利用方程解的定义找到相等关系，再把所求的代数式化简后整理出所找到的相等关系的形式，再把此相等关系整体代入所求代数式，即可求出代数式的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．解不等式组
    -5+$\frac{x}{3}$≥$\frac{4x+1}{8}$-$\frac{7}{2}$＞-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．一个三角形的三边长分别为9、12、15，那么两个这样的三角形拼成的四边形的面积为108．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知Rt△ABC中，a、b为直角边，c为斜边，h为斜边上的高，则下面说法错误的是（　　）
    A．ab=ch
    B．h＜a
    C．以ah、bh、ab为边的三角形是直角三角形
    D．以a+b、ab、c为边的三角形是直角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．在半径为13的⊙O中，弦AB∥CD，弦AB和CD的距离为7，且两弦在圆心O的异侧，若AB=24，则CD的长为2$\sqrt{165}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，AB=AC，CD⊥AB于点D，BE⊥AC于点E，BE与CD相交于点O，图中有3对全等的直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

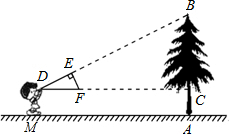    6．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与树顶点B在同一直线上．已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度DM=150cm，CD=800cm，则树高AB=550cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

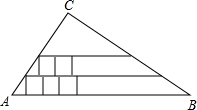    3．如图，已知在Rt△ABC中，∠C为直角，AC=5，BC=12，在Rt△ABC内从左往右叠放边长为1的正方形小纸片，第一层小纸片的一条边都在AB上，依次这样往上叠放上去，则最多能叠放22个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知a，b互为倒数，c，d互为相反数，x的倒数等于它本身，则ab-（c+d）+x的值为0或2．

    查看答案和解析>>

    同步练习册答案