
如图所示,一次函数y=k1x+b与反比例函数y= (x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(x<0)的图象相交于A,B两点,且与坐标轴的交点为(–6,0),(0,6),点B的横坐标为–4.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式k1x+b> 的解.
的解.
(1) ;(2) 6;(3) -4<x<-2.
;(2) 6;(3) -4<x<-2.
解析试题分析:(1)根据待定系数法就可以求出函数的解析式;
(2)求△AOB的面积就是求A,B两点的坐标,将一次函数与反比例函数的解析式组成方程即可求得;
(3)观察图象即可求得一次函数比反比例函数大的区间.
试题解析:(1)设一次函数解析式为y=kx+b,
∵一次函数与坐标轴的交点为(-6,0),(0,6),
∴ 解得:
解得: ,
,
∴一次函数关系式为:y=x+6,
∴B(-4,2),
∴反比例函数关系式为: ;
;
(2)∵点A与点B是反比例函数与一次函数的交点,
∴ ,
,
解得:x=-2或x=-4,
∴A(-2,4),
∴S△AOB=6×6÷2-6×2=6;
(3)-4<x<-2.
考点: 反比例函数与一次函数的交点问题.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
如图,一次函数y1=kx+b的图象与反比例函数y2= 的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).
(1)求这两个函数的解析式;
(2)当x取何值时, <
< .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,2),点P2(3,5),因为|1﹣3|<|2﹣5|,所以点P1与点P2的“非常距离”为|2﹣5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).
(1)已知点A(﹣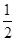 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知C是直线y= x+3上的一个动点,
x+3上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应的点E与点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在同一直角坐标系中反比例函数y= 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为 cm,则
cm,则 应是
应是 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| | 第一套 | 第二套 |
椅子高度 (cm) (cm) | 40 | 37 |
课桌高度 (cm) (cm) | 75 | 70 |
 与
与 的函数关系式.
的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与 轴围成的三角形的面积.
轴围成的三角形的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com