
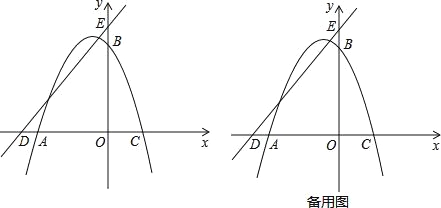
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌХзЮяЯпy=ax2+2xa+cОЙ§AЃЈЉ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉСНЕуЃЌгыxжсНЛгкСэвЛЕуCЃЌжБЯпy=x+5гыxжсНЛгкЕуDЃЌгыyжсНЛгкЕуEЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧЕкЖўЯѓЯоХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌСЌНгEPЃЌЙ§ЕуEзїEPЕФДЙЯпlЃЌдкlЩЯНиШЁЯпЖЮEFЃЌЪЙEF=EPЃЌЧвЕуFдкЕквЛЯѓЯоЃЌЙ§ЕуFзїFMЁЭxжсгкЕуMЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЯпЖЮFMЕФГЄЖШЮЊdЃЌЧѓdгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§ЕуEзїEHЁЭEDНЛMFЕФбгГЄЯпгкЕуHЃЌСЌНгDHЃЌЕуGЮЊDHЕФжаЕуЃЌЕБжБЯпPGОЙ§ACЕФжаЕуQЪБЃЌЧѓЕуFЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉd=5+tЃЛЃЈ3ЃЉF
ЃЛЃЈ2ЃЉd=5+tЃЛЃЈ3ЃЉF![]() .
.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉжБНгАбAЁЂBзјБъДњШыЧѓГіaЁЂcЕУжЕМДПЩЃЛЃЈ2ЃЉЗжБ№Й§PЁЂFЯђyжсзїДЙЯпЃЌДЙзуЗжБ№ЮЊAЁфЁЂBЁфЃЌЙ§PзїPNЁЭxжсЃЌДЙзуЮЊNЃЌвзжЄЁїPEAЁфЁеЁїEFBЁфЃЌПЩЕУГіd=FM=OEЉEBЁфЃЌдйДњШыПЩЧѓЕУНтЮіЪНЃЛЃЈ3ЃЉЯШЧѓЕУFЁЂHЕФзјБъЃЌЗЂЯжЕуPКЭЕуHЕФзнзјБъЯрЕШЃЌдђPHгыxжсЦНааЃЌИљОнЦНааЯпНиЯпЖЮГЩБШР§ЖЈРэПЩЕУGвВЪЧPQЕФжаЕуЃЌгЩДЫБэЪОГіЕуGЕФзјБъВЂСаЪНЃЌЧѓГіtЕФжЕВЂШЁЩсЃЌМЦЫуГіЕуFЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ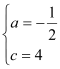 ЃЌЁрХзЮяЯпНтЮіЪНЮЊ
ЃЌЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЛЃЈ2ЃЉЗжБ№Й§PЁЂFЯђyжсзїДЙЯпЃЌДЙзуЗжБ№ЮЊAЁфЁЂBЁфЃЌЙ§PзїPNЁЭxжсЃЌДЙзуЮЊNЃЌЕБx=0ЪБЃЌy=5ЃЌЁрEЃЈ0ЃЌ5ЃЉЃЌЁрOE=5ЃЌЁпЁЯPEO+ЁЯOEF=90ЁуЃЌЁЯPEO+ЁЯEPAЁф=90ЁуЃЌЁрЁЯEPAЁф=ЁЯOEFЃЌЁпPE=EFЃЌЁЯEAЁфP=ЁЯEBЁфF=90ЁуЃЌЁрЁїPEAЁфЁеЁїEFBЁфЃЌЁрPAЁф=EBЁф=ЉtЃЌЁрd=FM=OBЁф=OEЉEBЁф=5ЉЃЈЉtЃЉ=5+tЃЛ
ЃЛЃЈ2ЃЉЗжБ№Й§PЁЂFЯђyжсзїДЙЯпЃЌДЙзуЗжБ№ЮЊAЁфЁЂBЁфЃЌЙ§PзїPNЁЭxжсЃЌДЙзуЮЊNЃЌЕБx=0ЪБЃЌy=5ЃЌЁрEЃЈ0ЃЌ5ЃЉЃЌЁрOE=5ЃЌЁпЁЯPEO+ЁЯOEF=90ЁуЃЌЁЯPEO+ЁЯEPAЁф=90ЁуЃЌЁрЁЯEPAЁф=ЁЯOEFЃЌЁпPE=EFЃЌЁЯEAЁфP=ЁЯEBЁфF=90ЁуЃЌЁрЁїPEAЁфЁеЁїEFBЁфЃЌЁрPAЁф=EBЁф=ЉtЃЌЁрd=FM=OBЁф=OEЉEBЁф=5ЉЃЈЉtЃЉ=5+tЃЛ
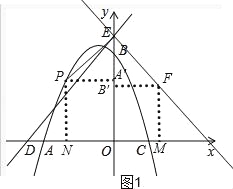
ЃЈ3ЃЉШчЭМЃЌгЩжБЯпDEЕФНтЮіЪНЮЊЃКy=x+5ЃЌЁпEHЁЭEDЃЌЁржБЯпEHЕФНтЮіЪНЮЊЃКy=Љx+5ЃЌ
ЁрFBЁф=AЁфE=5ЉЃЈЉ![]() t2Љt+4ЃЉ=
t2Љt+4ЃЉ=![]() t2+t+1ЃЌЁрFЃЈ
t2+t+1ЃЌЁрFЃЈ![]() t2+t+1ЃЌ5+tЃЉЃЌЁрЕуHЕФКсзјБъЮЊЃК
t2+t+1ЃЌ5+tЃЉЃЌЁрЕуHЕФКсзјБъЮЊЃК![]() t2+t+1ЃЌ
t2+t+1ЃЌ
y=Љ![]() t2ЉtЉ1+5=Љ
t2ЉtЉ1+5=Љ![]() t2Љt+4ЃЌЁрHЃЈ
t2Љt+4ЃЌЁрHЃЈ![]() t2+t+1ЃЌЉ
t2+t+1ЃЌЉ![]() t2Љt+4ЃЉЃЌЁпGЪЧDHЕФжаЕуЃЌЁрGЃЈ
t2Љt+4ЃЉЃЌЁпGЪЧDHЕФжаЕуЃЌЁрGЃЈ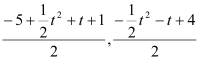 ЃЉЃЌМДGЃЈ
ЃЉЃЌМДGЃЈ![]() t2+
t2+![]() tЉ2ЃЌЉ
tЉ2ЃЌЉ![]() t2Љ
t2Љ![]() t+2ЃЉЃЌЁрPHЁЮxжсЃЌЁпDG=GHЃЌЁрPG=GQЃЌ
t+2ЃЉЃЌЁрPHЁЮxжсЃЌЁпDG=GHЃЌЁрPG=GQЃЌ
Ёр![]() ЃЌНтЕУt=
ЃЌНтЕУt=![]() ЃЌЁпPдкЕкЖўЯѓЯоЃЌЁрtЃМ0ЃЌЁрt=
ЃЌЁпPдкЕкЖўЯѓЯоЃЌЁрtЃМ0ЃЌЁрt=![]() ЃЌЁрFЃЈ
ЃЌЁрFЃЈ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖрЯюЪНyЃxyЃЋ2ЕФЯюЪ§ЁЂДЮЪ§ЗжБ№ЪЧ( )
A. 3ЃЌ2 B. 3ЃЌ4
C. 3ЃЌ3 D. 2ЃЌ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
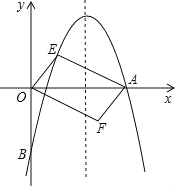
ЁОЬтФПЁПШчЭМЃЌЖдГЦжсЮЊжБЯпx=ЕФХзЮяЯпОЙ§ЕуAЃЈ6ЃЌ0ЃЉКЭBЃЈ0ЃЌЉ4ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАЖЅЕузјБъЃЛ
ЃЈ2ЃЉЩшЕуEЃЈxЃЌyЃЉЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЧвЮЛгкЕквЛЯѓЯоЃЌЫФБпаЮOEAFЪЧвдOAЮЊЖдНЧЯпЕФЦНааЫФБпаЮЃЌЧѓЦНааЫФБпаЮOEAFЕФУцЛ§SгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕБЃЈ2ЃЉжаЕФЦНааЫФБпаЮOEAFЕФУцЛ§ЮЊ24ЪБЃЌЧыХаЖЯЦНааЫФБпаЮOEAFЪЧЗёЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЪЧЪщЗЈаЁзщФГДЮВтбщЕФГЩМЈЭГМЦБэЃЎдђГЩМЈЕФжкЪ§ЪЧЃЈ ЁЁ ЃЉ
ГЩМЈ/Зж | 7 | 8 | 9 | 10 |
ШЫЪ§/ШЫ | 4 | 3 | 2 | 1 |
A.1B.4C.7D.8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕуMЃЈxЃЌЉ4ЃЉгыЕуNЃЈ2ЃЌyЃЉЙигкyжсЖдГЦЃЌдђxЉyЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. Љ6 B. 6 C. 2 D. Љ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
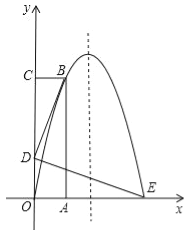
ЁОЬтФПЁПШчЭМЃЌГЄЗНаЮOABCЕФOAБпдкxжсЕФе§АыжсЩЯЃЌOCдкyжсЕФе§АыжсЩЯЃЌХзЮяЯпy=ax2+bxОЙ§ЕуBЃЈ1ЃЌ4ЃЉКЭЕуEЃЈ3ЃЌ0ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуDдкЯпЖЮOCЩЯЃЌЧвBDЁЭDEЃЌBD=DEЃЌЧѓDЕуЕФзјБъЃЛ
ЃЈ3ЃЉдкЬѕМўЃЈ2ЃЉЯТЃЌдкХзЮяЯпЕФЖдГЦжсЩЯеввЛЕуMЃЌЪЙЕУЁїBDMЕФжмГЄЮЊзюаЁЃЌВЂЧѓЁїBDMжмГЄЕФзюаЁжЕМАДЫЪБЕуMЕФзјБъЃЛ
ЃЈ4ЃЉдкЬѕМўЃЈ2ЃЉЯТЃЌДгBЕуЕНEЕуетЖЮХзЮяЯпЕФЭМЯѓЩЯЃЌЪЧЗёДцдквЛИіЕуPЃЌЪЙЕУЁїPADЕФУцЛ§зюДѓЃПШєДцдкЃЌЧыЧѓГіЁїPADУцЛ§ЕФзюДѓжЕМАДЫЪБPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ2x2Љ2y2ЃЉЉ3ЃЈx2y2+x2ЃЉ+3ЃЈx2y2+y2ЃЉЃЌЦфжаx=Љ1ЃЌy=2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЕуP(aЃЌb)дкЕкШ§ЯѓЯоЃЌдђЕуQ(ЃaЃЌЃb)дкЕк________ЯѓЯоЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com