
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)请问一元二次方程x2﹣3x+2=0是倍根方程吗?如果是,请说明理由.
(2)若一元二次方程ax2+bx﹣6=0是倍根方程,且方程有一个根为2,求a、b的值?
【答案】
(1)解:是倍根方程,理由如下:
解方程x2﹣3x+2=0,得x1=1,x2=2,
∵2是1的2倍,
∴一元二次方程x2﹣3x+2=0是倍根方程
(2)解:分两种情况:
①另外一个根为4时,
﹣ ![]() =2+4,﹣
=2+4,﹣ ![]() =2×4,
=2×4,
∴a=﹣ ![]() ,b=
,b= ![]() ;
;
②另外一个根为1时,
﹣ ![]() =2+1,﹣
=2+1,﹣ ![]() =2×1,
=2×1,
∴a=﹣3,b=9
【解析】(1)利用因式分解法求出方程的两根,再根据倍根方程的定义判断即可;(2)根据倍根方程的定义,倍根方程ax2+bx﹣6=0有一个根为2时,另外一个根为4或1,再利用根与系数的关系求出a、b的值.
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
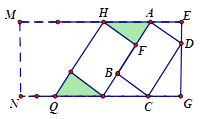
【题目】如图,在一个矩形停车场MNGE中,矩形ABCD是一辆机动车停放的车位示意图,经测量得AB=5.4米,BC=2.4米,AF=1.8米,HF⊥AB.其中HF是另一车位的一边,所有车位尺寸一样,并按图示并列划定.
(1)求路宽EG;
(2)若停车场的长EM=85米,求这个停车场的停车车位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的表示如图所示,则下列结论中: ①ab<0, ②![]() <0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
<0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
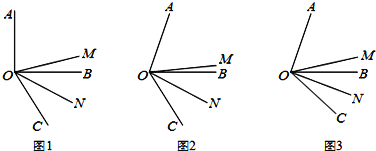
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果).
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON= (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣(t﹣4)2+20.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3sB.4sC.5sD.6s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花园的护栏都是用直径![]() 的半圆形条钢组制而成,且每增加一个半圆形条钢,半圆护栏长度增加
的半圆形条钢组制而成,且每增加一个半圆形条钢,半圆护栏长度增加![]() ,(
,( ![]() )设半圆形条钢的总个数为
)设半圆形条钢的总个数为![]() (
(![]() 为正整数),护栏总长为
为正整数),护栏总长为![]() .
.
(![]() )当
)当![]() 时,用
时,用![]() 的代数式表示
的代数式表示![]() .
.
(![]() )若护栏总长度为
)若护栏总长度为![]() ,当
,当![]() 时,所用半圆形条钢的个数.
时,所用半圆形条钢的个数.
(![]() )若护栏的总长度不变,则当
)若护栏的总长度不变,则当![]() 时,用了
时,用了![]() 个半圆形条钢,当
个半圆形条钢,当![]() 时,用了
时,用了![]() 个半圆形条钢,请用含
个半圆形条钢,请用含![]() 的代数式表示
的代数式表示![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若存在3个互不相同的有理数a,b,c,使得|1﹣a|+|1﹣3a|+|1﹣4a|=|1﹣b|+|1﹣3b|+|1﹣4b|=|1﹣c|+|1﹣3c|+|1﹣4c|=t,则t=
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com