
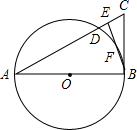
 如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=
如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
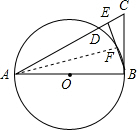 (1)证明:连接AF.
(1)证明:连接AF.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
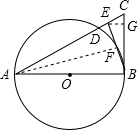
| CE |
| CA |
| EG |
| AB |
| CE |
| CE+8 |
| 1 |
| 8 |
| 8 |
| 7 |
| 8 |
| 7 |
| 64 |
| 7 |


科目:初中数学 来源: 题型:
 北京时间2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线y=-
北京时间2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线y=-| 1 |
| 250 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
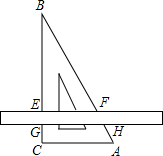 如图,将直尺垂直三角板ABC的直角边BC放置,直尺的一边被三角板截出的边长EF=
如图,将直尺垂直三角板ABC的直角边BC放置,直尺的一边被三角板截出的边长EF=10
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com