
 ;(2)
;(2)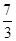 ;(3)(1,
;(3)(1,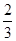 ).
).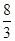 -2=
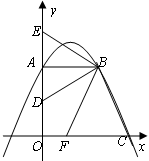
-2=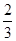 .由EA⊥AB,GH⊥AB,可得GH是△BEA的中位线,从而可得EA=3GH=
.由EA⊥AB,GH⊥AB,可得GH是△BEA的中位线,从而可得EA=3GH=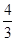 .过B作BM⊥OC,垂足为M.MB=OA=AB.由∠EBF=∠ABM=90°,可得∠EBA=∠FBM=90°-∠ABF.即可证得Rt△EBA≌Rt△FBM.再根据全等三角形的性质即可求得结果;
.过B作BM⊥OC,垂足为M.MB=OA=AB.由∠EBF=∠ABM=90°,可得∠EBA=∠FBM=90°-∠ABF.即可证得Rt△EBA≌Rt△FBM.再根据全等三角形的性质即可求得结果;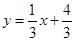 .再求的直线
.再求的直线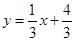 与对称轴x=1的交点即为点Q,坐标为(1,
与对称轴x=1的交点即为点Q,坐标为(1,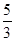 ).从而得到结果.
).从而得到结果.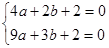 解得
解得 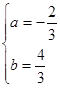
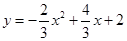 ;
;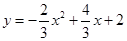 =
=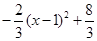 .
.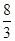 ).
).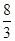 -2=
-2=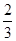 .
.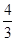 .
.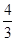 .
.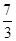 ;
;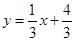 .
. 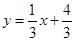 与对称轴x=1的交点即为点Q,坐标为(1,
与对称轴x=1的交点即为点Q,坐标为(1,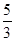 ).点P的坐标为(1,
).点P的坐标为(1,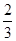 ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
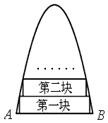
| A.第七块 | B.第六块 | C.第五块 | D.第四块 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 时,求直线AN的解析式.
时,求直线AN的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
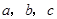 ,用
,用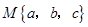 表示这三个数的平均数,用
表示这三个数的平均数,用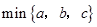 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: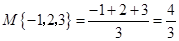 ;
;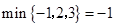 ;
;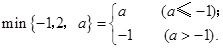
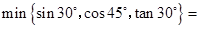 ;
;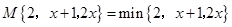 ,求
,求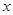 ;
; ,那么 (填
,那么 (填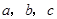 的大小关系)”.
的大小关系)”.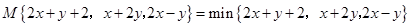 ,则
,则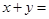 .
.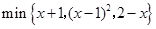 的最大值为 .
的最大值为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
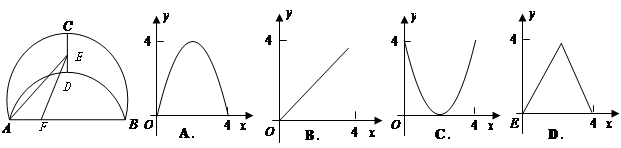
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
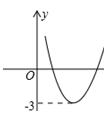
| A.无实数根 | B.有两个相等实数根 |
| C.有两个异号实数根 | D.有两个同号不等实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com