练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
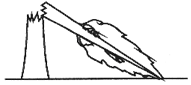
    9．如图，一场大风后，一棵大树在高于地面1米处折断，大树顶部落在距离大树底部3米处的地面上，那么树高是（　　）
    A．4mB．$\sqrt{10}$mC．（$\sqrt{10}$+1）mD．（$\sqrt{10}$+3）m

    分析 首先根据勾股定理求得折断的树高，继而即可求出折断前的树高．

    解答 解：根据勾股定理可知：折断的树高=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$米，
    则这棵大树折断前的树高=（1+$\sqrt{10}$）米．
    故选C．

    点评 考查了利用勾股定理解应用题，关键在于把折断部分、大树原来部分和地面看作一个直角三角形，利用勾股定理列出方程求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．判断下面说法是否正确，并举例说明理由．
    （1）两个无理数的和一定是无理数；
    （2）两个无理数的积一定是无理数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．若|x|=4，|y|=3，则|x+y|的值为（　　）
    A．7B．-7C．7或1D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

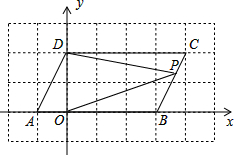    17．在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（b，0），且a，b满足|a+b-2|+$\sqrt{2a-b+5}$=0，现同时将点A，B分别向右平移1个单位，再向上平移2个单位，分别得到点A，B的对应点为C，D．
    （1）请直接写出A、B、C、D四点的坐标并在坐标系中画出点A、B、C、D，连接AC，BD，CD．
    （2）点E在坐标轴上，且S△BCE=S四边形ABDC，求满足条件的点E的坐标．
    （3）点P是线段BD上的一个动点，连接PC，PO，当点P在线段BD上移动时（不与B，D重合）证明：$\frac{∠DCP+∠BOP}{∠CPO}$是个常数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

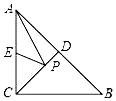    4．如图，Rt△ABC中，AC=BC=4，点D，E分别是AB，AC的中点，在CD上找一点P，使PA+PE最小，则这个最小值是（　　）
    A．2B．$2\sqrt{2}$C．$2\sqrt{5}$D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．将分别标有数字2，3，5的三张质地，大小完全一样的卡片背面朝上放在桌面上．随机抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字．画树状图或列表写出组成的所有的两位数，并求出抽取到的两位数恰好是35的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．$\frac{4}{9}$的倒数是$\frac{9}{4}$，绝对值是$\frac{4}{9}$，相反数是-$\frac{4}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．38°41′的角的余角等于51°19′，27°14′24″=27.24度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

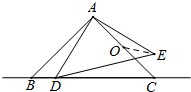    19．如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=4，O为AC中点，若点D在直线BC上运动，连接OE，则在点D运动过程中，线段OE的最小值是为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．1D．$\sqrt{2}$

    查看答案和解析>>

    同步练习册答案