
 如图,AD是△ABC的中线,E是AD的中点,BE的延长线交AC于点F,若FC=12,AF的长为( )
如图,AD是△ABC的中线,E是AD的中点,BE的延长线交AC于点F,若FC=12,AF的长为( )| A. | 4 | B. | 6 | C. | 10 | D. | 8 |
分析 如图,作辅助线;得到△BDE∽△BCG,△AEF∽△CGF,运用相似三角形的性质,列出比例式,找出线段CG、
AE、CF、AF之间的数量关系,即可解决问题.
解答 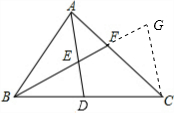 解:如图,过点C作CG∥AD,交BF的延长线于点G;
解:如图,过点C作CG∥AD,交BF的延长线于点G;
则△BDE∽△BCG,△AEF∽△CGF,
∴$\frac{CG}{DE}=\frac{BC}{BD}$①,$\frac{CG}{AE}=\frac{CF}{AF}$②
∵BD=CD,AE=DE,
∴由①、②知:$\frac{CF}{AF}$=2,而CF=12,
∴AF=6,
故选B.
点评 该题主要考查了相似三角形的判定、三角形的中位线定理等几何知识点及其应用问题;解题的关键是作平行线,构造相似三角形,灵活运用相似三角形的判定、三角形的中位线定理等几何知识点来分析、解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
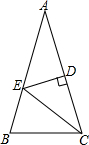 如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )
如图,在△ABC,∠A=36°,∠B=72°,AC的垂直平分线分别交AC、AB于点D,E,则图中等腰三角形的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
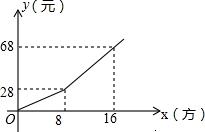 为鼓励市民节约用水,某市自来水公司按分段收费标准收费,如图反映的是每月所收水费y(元)与用水量x(方)之间的函数关系.
为鼓励市民节约用水,某市自来水公司按分段收费标准收费,如图反映的是每月所收水费y(元)与用水量x(方)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
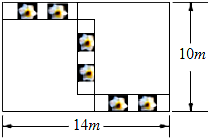 某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为( )
某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为( )| A. | 8 | B. | 13 | C. | 16 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com