

 α+
α+ ∠ABC=∠A1+
∠ABC=∠A1+ ∠ABC,即:∠A1=
∠ABC,即:∠A1= α;
α;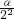 ; …;∠A7=
; …;∠A7=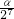 =
=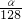 ,
,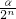 .
. .
. α+
α+ ∠ABC=∠A1+
∠ABC=∠A1+ ∠ABC,求出∠A1=
∠ABC,求出∠A1= α;再求出∠A2,即可得出规律,求出即可.
α;再求出∠A2,即可得出规律,求出即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 明码 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 13 | 24 | 25 | 26 |
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y= | |||||
| 密码:y | 91 | 40 | |||
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y=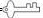 | |||||
| 密码:y | 70 | 36 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 明码 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 13 | 24 | 25 | 26 |
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y= | |||||
| 密码:y | 91 | 40 | |||
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y= | |||||
| 密码:y | 70 | 36 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下列材料:
我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离;即![]() ,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;
,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;
这个结论可以推广为![]() 表示在数轴上
表示在数轴上![]() ,
,![]() 对应点之间的距离;
对应点之间的距离;
例1 解方程![]() ,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
例2 解不等式▏x-1▏>2,如图,在数轴上找出▏x-1▏=2的解,即到1的距离为2的点对应的数为-1、3,则▏x-1▏>2的解为x<-1或x>3

例3 解方程![]() 。由绝对值的几何意义知,该方程表示求在数轴上与1
。由绝对值的几何意义知,该方程表示求在数轴上与1
和-2的距离之和为5的点对应的x的值。在数轴上,1和-2的距离为3,满足方程的x对应点在1的右边或-2的左边,若x对应点在1的右边,由图可以看出x=2;同理,若x对应点在-2的左边,可得x=-3,故原方程的解是x=2或x=-3

参考阅读材料,解答下列问题:
(1)方程![]() 的解为
的解为
(2)解不等式![]() ≥9;
≥9;
(3)若![]() ≤a对任意的x都成立,求a的取值范围.
≤a对任意的x都成立,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下列材料并解答。
例 平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
(2)归纳:考察点的个数和可连成直线的条数![]() 发现:如下表
发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
(3)推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,
故应除以2;即![]()
(4)![]() 结论:
结论:![]()
![]()
试探究以下几个问题:
平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数![]() ,发现:(填下表)
,发现:(填下表)
| 点的 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n |
( 3 ) 推理:
(4)结论:
查看答案和解析>>
科目:初中数学 来源:2009年辽宁省沈阳市中考数学试卷(解析版) 题型:解答题
| 字母 | A | B | C | D | E | F | G | H | I | J | K | L | M |
| 明码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 明码 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 13 | 24 | 25 | 26 |
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y= | |||||
| 密码:y | 91 | 40 | |||
| 汉字 | 自 | 信 | |||
| 拼音 | Z | I | X | I | N |
| 明码:x | 26 | 9 | 24 | 9 | 14 |
密钥:y= | |||||
| 密码:y | 70 | 36 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com