
| 2 |
3±
| ||
| 2×1 |
3±
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
4±
| ||
| 2×3 |
2±
| ||
| 3 |
2+
| ||
| 3 |
2-
| ||
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 16 |
| 1 |
| 2 |
2
| ||||
| 2×1 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山东临沭第三初级中学九年级10月月考数学试卷(带解析) 题型:解答题
阅读下面例题的解答过程,体会并其方法,并借鉴例题的解法解方程。
例:解方程x2- -1=0.
-1=0.
解:(1)当x-1≥0即x≥1时, = x-1。
= x-1。
原化为方程x2-(x-1)-1=0,即x2-x=0
解得x1 =0.x2=1
∵x≥1,故x =0舍去,
∴x=1是原方程的解。
(2)当x-1<0即x<1时, =-(x-1)。
=-(x-1)。
原化为方程x2+(x-1)-1=0,即x2+x-2=0
解得x1 =1.x2=-2
∵x<1,故x =1舍去,
∴x=-2是原方程的解。
综上所述,原方程的解为x1 =1.x2=-2
解方程x2- -4=0.
-4=0.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山东临沭第三初级中学九年级10月月考数学试卷(解析版) 题型:解答题
阅读下面例题的解答过程,体会并其方法,并借鉴例题的解法解方程。
例:解方程x2- -1=0.
-1=0.
解:(1)当x-1≥0即x≥1时, = x-1。
= x-1。
原化为方程x2-(x-1)-1=0,即x2-x=0
解得x1 =0.x2=1
∵x≥1,故x =0舍去,
∴x=1是原方程的解。
(2)当x-1<0即x<1时, =-(x-1)。
=-(x-1)。
原化为方程x2+(x-1)-1=0,即x2+x-2=0
解得x1 =1.x2=-2
∵x<1,故x =1舍去,
∴x=-2是原方程的解。
综上所述,原方程的解为x1 =1.x2=-2
解方程x2- -4=0.
-4=0.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
关于x的方程:x+ =c+
=c+ 的解是x1=c,x2=
的解是x1=c,x2= ;
;
x- =c-
=c- (即x+
(即x+ =c+
=c+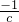 )的解是x1=c,x2=-
)的解是x1=c,x2=- ;
;
x+ =c+
=c+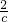 的解是:x1=c,x2=
的解是:x1=c,x2=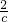 ,…
,…
(1)观察上述方程及其解的特征,直接写出关于x的方程x+ =c+
=c+ (m≠0)的解,并利用“方程的解”的概念进行验证;
(m≠0)的解,并利用“方程的解”的概念进行验证;
(2)通过(1)的验证所获得的结论,你能解出关于x的方程:x+ =a+
=a+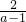 的解吗?若能,请求出此方程的解;若不能,请说明理由.
的解吗?若能,请求出此方程的解;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2009年北京市通州区中考数学二模试卷(解析版) 题型:解答题
 =c+
=c+ 的解是x1=c,x2=
的解是x1=c,x2= ;
; =c-
=c- (即x+
(即x+ =c+
=c+ )的解是x1=c,x2=-
)的解是x1=c,x2=- ;x+
;x+ =c+
=c+ 的解是:x1=c,x2=
的解是:x1=c,x2= ,…
,… =c+
=c+ (m≠0)的解,并利用“方程的解”的概念进行验证;
(m≠0)的解,并利用“方程的解”的概念进行验证; =a+
=a+ 的解吗?若能,请求出此方程的解;若不能,请说明理由.
的解吗?若能,请求出此方程的解;若不能,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com