
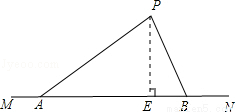
(本题满分10分)如图,海岸线MN上有A,B两艘船,均收到已触角搁浅的船P求救信号﹒经测量,∠PAB=37°, ∠PBA=67°,AB的距离为42海里﹒

(1)求船P到海岸线MN的距离;
(2)若船A,船B分别以20海里/时,15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断那艘船先到达船P处﹒
(参考数据:sin67°≈ ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,Sin37°≈
,Sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
(1)PE=24海里;
(2)B船先到达P处.
【解析】
试题分析:(1)过点P作PE⊥AB于点E,在Rt△APE和Rt△BPE中解出PE即可;
(2)在Rt△BPF中,求出BP,分别计算出两艘船需要的时间,即可作出判断
试题解析:(1)如图:过点P作PE⊥AB于点E,
在Rt△APE中,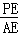 =tan37°,
=tan37°,
AE=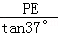 ;
;
在Rt△BPE中,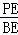 =tan67°,
=tan67°,
BE=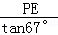 ;
;
∴AE+EB=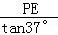 +
+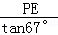 =42,
=42,
∴ +
+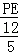 ≈42,
≈42,
∴(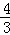 +
+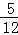 )PE≈42,
)PE≈42,
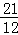 PE≈42,
PE≈42,
PE≈42×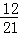 =24.
=24.
(2)在Rt△APE中,sin37°=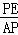 ,
,
∴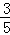 ≈
≈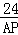 ,
,
解得AP≈40海里;
A船所用时间为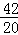 =
=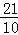 小时;
小时;
在Rt△BPE中,sin67°=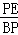 ,
,
∴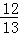 ≈
≈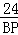 ,
,
解得BP≈26海里;
B船所用时间为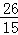 小时;
小时;
∴B船先到达P处.
考点:解直角三角形的应用


科目:初中数学 来源:2015届山东省八年级上学期期中数学试卷(解析版) 题型:填空题
已知实数a、b满足:a+b=2,a-b=5,则(a+b)3·(a-b)3的值是___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省等九年级上学期第三次月考数学试卷(解析版) 题型:解答题
某商品的进价为每件40元,售价为每件50元,每个月可卖出200件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于进价的140%).设每件商品的售价上涨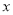 元(
元(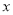 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为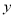 元.
元.
(1)求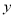 与
与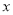 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量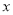 的取值范围;
的取值范围;
(2)每件商品的售价m定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
⑶每件商品的售价m定为多少元时,每个月的利润恰为2160元?根据以上结论,请你直接写出售价m在什么范围时,每个月的利润不低于2160元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省等九年级上学期第三次月考数学试卷(解析版) 题型:填空题
若两个等边三角形的边长分别为a与3a,则它们的面积之比为___________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省等九年级上学期第三次月考数学试卷(解析版) 题型:选择题
方程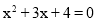 的根的情况是( )
的根的情况是( )
A.有两个相等实数根
B.有两个不相等实数根
C.有一个实数根
D.无实数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com