

分析 (1)设小亮从乙地到甲地过程中y2(米)与x(分钟)之间的函数关系式为y2=k2x+b,由待定系数法根据图象就可以求出解析式;
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象.
解答 解:(1)设小亮从乙地到甲地过程中y2(米)与x(分钟)之间的函数关系式为y2=k2x+b,由图象,得
$\left\{\begin{array}{l}{2000=b}\\{0=10{k}_{2}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-200}\\{b=2000}\end{array}\right.$,
∴y2=-200x+2000;
(2)由题意,得
小明的速度为:2000÷40=50米/分,
小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为(24×50)÷(200-50)=8分钟,
∴24分钟时两人的距离为:S=24×50=1200,32分钟时S=0,
设S与x之间的函数关系式为:S=kx+b1,由题意,得
$\left\{\begin{array}{l}{1200=24k+{b}_{1}}\\{0=32k+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-150}\\{{b}_{1}=4800}\end{array}\right.$,
∴S=-150x+4800(24≤x≤32);
(3)由题意,得
a=2000÷(200+50)=8分钟,
当x=24时,S=1200,
设经过x分钟追上小明,则200x-50x=1200,解得x=8,此时的总时间就是24+8=32分钟.
故描出相应的点就可以补全图象.
如图: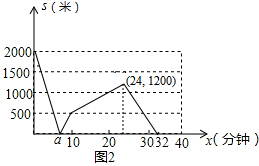
点评 本题考查了待定系数法求一次函数的解析式的运用,追击问题与相遇问题在实际问题中的运用,描点法画函数图象的运用,解答时灵活运用路程、速度、时间之间的数量关系是关键.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象经过点A(1,4),B(m,n).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
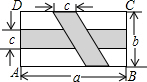 长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )
长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )| A. | bc-ab+ac+c2 | B. | ab-bc-ac+c2 | C. | a2+ab+bc-ac | D. | b2-bc+a2-ab |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
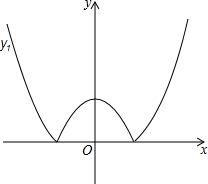 如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
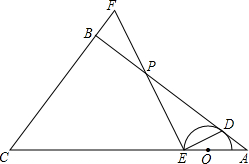 如图,在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,连接ED,过点E作ED的高,交射线AB于点P,交射线CB于点F.
如图,在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,连接ED,过点E作ED的高,交射线AB于点P,交射线CB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com