Question

【题目】如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

（1）出发2秒后，求PQ的长；
（2）从出发几秒钟后，△PQB第一次能形成等腰三角形？
（3）当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

Answer 1

【答案】
（1）解：BQ=2×2=4cm，

BP=AB﹣AP=8﹣2×1=6cm，

∵∠B=90°，

PQ= = = =2

（2）解：BQ=2t，

BP=8﹣t

2t=8﹣t，

解得：t=

（3）解：①当CQ=BQ时（图1），则∠C=∠CBQ，

∵∠ABC=90°，

∴∠CBQ+∠ABQ=90°，

∠A+∠C=90°，

∴∠A=∠ABQ，

∴BQ=AQ，

∴CQ=AQ=5，

∴BC+CQ=11，

∴t=11÷2=5.5秒．

②当CQ=BC时（如图2），则BC+CQ=12

∴t=12÷2=6秒．

③当BC=BQ时（如图3），过B点作BE⊥AC于点E，

则BE= = ，

所以CE= ，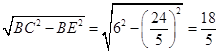

故CQ=2CE=7.2，

所以BC+CQ=13.2，

∴t=13.2÷2=6.6秒．

由上可知，当t为5.5秒或6秒或6.6秒时，

△BCQ为等腰三角形．

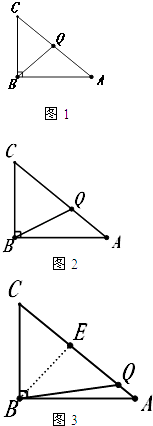
【解析】（1）根据点P、Q的运动速度求出AP，再求出BP和BQ，用勾股定理求得PQ即可；（2）设出发t秒钟后，△PQB能形成等腰三角形，则BP=BQ，由BQ=2t，BP=8﹣t，列式求得t即可；（3）当点Q在边CA上运动时，能使△BCQ成为等腰三角形的运动时间有三种情况：①当CQ=BQ时（图1），则∠C=∠CBQ，可证明∠A=∠ABQ，则BQ=AQ，则CQ=AQ，从而求得t；②当CQ=BC时（如图2），则BC+CQ=12，易求得t；③当BC=BQ时（如图3），过B点作BE⊥AC于点E，则求出BE，CE，即可得出t．
【考点精析】通过灵活运用三角形的面积和勾股定理的概念，掌握三角形的面积=1/2×底×高；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．