
【题目】已知抛物线C1:y=x2﹣(2m+4)x+m2﹣10的顶点A到y轴的距离为3,与x轴交于C、D两点.
(1)求顶点A的坐标;
(2)若点B在抛物线C1上,且![]() ,求点B的坐标.
,求点B的坐标.
【答案】
【1】 (1)(3,-18)
【2】 (2)![]()
【解析】
(1)把抛物线一般表达式写成顶点式,知道顶点A到y轴的距离,进而求出m的值,写出抛物线顶点式表达式,求出坐标.(2)由抛物线C1的解析式为y=(x-3)2-18,解得C、D两点坐标,求出CD的值,由B点在抛物线C1上,S△BCD=6![]() ,求出B点纵坐标,把纵坐标代入抛物线解出横坐标.
,求出B点纵坐标,把纵坐标代入抛物线解出横坐标.
解:(1)y=x2-(2m+4)x+m2-10
=[x-(m+2)]2+m2-10-(m+2)2
=[x-(m+2)]2-4m-14
∴抛物线顶点A的坐标为(m+2,-4m-14)
由于顶点A到y轴的距离为3,
∴|m+2|=3
∴m=1或m=-5
∵抛物线与x轴交于C、D两点,
∴m=-5舍去.
∴m=1,
∴抛物线顶点A的坐标为(3,-18).
(2)∵抛物线C1的解析式为y=(x-3)2-18,
∴抛物线C1与x轴交C、D两点的坐标为(3+3![]() ,0),(3?3
,0),(3?3![]() ,0),
,0),
∴CD=6![]() ,
,
∵B点在抛物线C1上,S△BCD=6![]() ,设B(xB,yB),则yB=±2,
,设B(xB,yB),则yB=±2,
把yB=2代入到抛物线C1的解析式为y=(x-3)2-18,
解得xB=2![]() +3或xB=?2
+3或xB=?2![]() +3,
+3,
把yB=-2代入到抛物线C1的解析式为y=(x-3)2-18,
解得xB=-1或xB=7,
∴B点坐标为(2![]() +3,2),(-2
+3,2),(-2![]() +3,2),(-1,-2),(7,-2)
+3,2),(-1,-2),(7,-2)


科目:初中数学 来源: 题型:
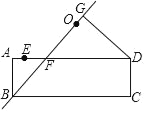
【题目】如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,
(1)求等边三角形的高;
(2)求CE的长度;
(3)若将等边三角形ABC绕点C顺时针旋转,旋转角为α(0°<α<360°),求α为多少时,等边三角形的边所在的直线与圆相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
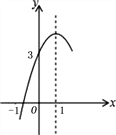
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① 4ac<b2;② 方程ax2+bx+c=0的两个根是![]() ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
其中结论正确有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是![]() 的中点.
的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 的“
的“![]() 值”定义如下:若点
值”定义如下:若点![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点![]() 的“
的“![]() 值”,记为
值”,记为![]() .特别的,当点
.特别的,当点![]() ,
, ![]() 重合时,线段
重合时,线段![]() 的长度为0.
的长度为0.
当⊙![]() 的半径为2时:
的半径为2时:
(1)若点![]() ,
, ![]() ,则
,则![]() _________,
_________, ![]() _________;
_________;
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求出点
,求出点![]() 的横坐标;
的横坐标;
(3)直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点
轴分别交于点![]() ,
, ![]() .若线段
.若线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请你直接写出
,请你直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com