
【题目】一个边长为4的等边三角形ABC的高与⊙O的直径相等,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,
(1)求等边三角形的高;
(2)求CE的长度;
(3)若将等边三角形ABC绕点C顺时针旋转,旋转角为α(0°<α<360°),求α为多少时,等边三角形的边所在的直线与圆相切.

【答案】(1)2![]() ;(2)3;(3)α=60°或120°或180°或300°.
;(2)3;(3)α=60°或120°或180°或300°.
【解析】
(1)作AM⊥MC于M,在直角三角形ACM中,利用勾股定理即可解题,
(2)连接EF,在直角三角形CEF中, 利用勾股定理即可解题,
(3)画出图形即可解题.
解:(1)如图,作AM⊥MC于M.
∵△ABC是等边三角形,
∴∠MAC=∠MAB=30°,
∴CM=![]() AC=2,
AC=2,
∴AM=![]() =
=![]() =2
=2![]()
(2)∵CF是⊙O直径,
∴CF=CM=2![]() ,连接EF,则∠CEF=90°,
,连接EF,则∠CEF=90°,
∵∠ECF=90°﹣∠ACB=30°,
∴EF=![]() CF=
CF=![]() ,
,
∴CE=![]() =
=![]() =3.
=3.
(3)由图象可知,α=60°或120°或180°或300°时,等边三角形的边所在的直线与圆相切.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
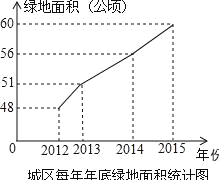
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
(1)根据图中所提供的信息回答下列问题:2015年底的绿地面积为 公顷,比2014年底增加了 公顷;在2013年,2014年,2015年这三年中,绿地面积增加最多的是 年;
(2)为满足城市发展的需要,计划到2017年底使城区绿地面积达到72.6公顷,试求今明两年绿地面积的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
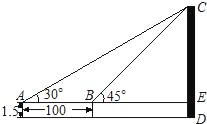
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ | … | ﹣5 | ﹣3 | 2 | … |
植物高度增长量h/mm | … | 34 | 46 | 41 | … |
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=x2﹣(2m+4)x+m2﹣10的顶点A到y轴的距离为3,与x轴交于C、D两点.
(1)求顶点A的坐标;
(2)若点B在抛物线C1上,且![]() ,求点B的坐标.
,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点的坐标为(![]() ,1),下列结论:①c>0;②b2﹣4ac>0;③a+b=0;④4ac﹣b2>4a,其中错误的是( )
,1),下列结论:①c>0;②b2﹣4ac>0;③a+b=0;④4ac﹣b2>4a,其中错误的是( )
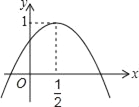
A. ① B. ② C. ③ D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com