
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是______.
科目:初中数学 来源: 题型:
【题目】某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图所示,这是某校八(1)班教室简图,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别代表五个学习小组的位置.已知
分别代表五个学习小组的位置.已知![]() 点的坐标为(-1,3).
点的坐标为(-1,3).
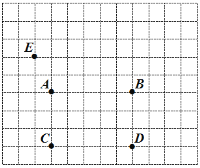
(1)请按题意建立平面直角坐标系(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度),写出图中其他几个学习小组的坐标;
(2)若(1)中建立的平面直角坐标系坐标原点为![]() ,点
,点![]() 在
在![]() 的延长线上,请写出
的延长线上,请写出![]() 、
、![]() 、
、![]() 之间的等量关系,并说明原因.
之间的等量关系,并说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一元二次方程![]() 中,若系数
中,若系数![]() 和
和![]() 可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元

(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°.将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON= ,∠CON= ;
(3)若∠BOC=α,∠NOC=β,将三角板MON绕点O逆时针旋转至图③时,求∠AOM.
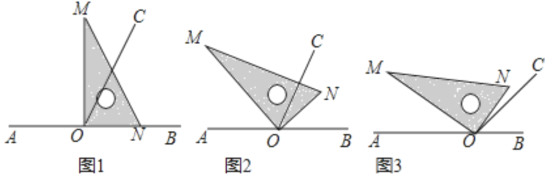
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt![]() 中,∠BAC=90°且AB=AC,D是边BC上一点,E是边AC上一点,AD=AE,若
中,∠BAC=90°且AB=AC,D是边BC上一点,E是边AC上一点,AD=AE,若![]() 为等腰三角形,则∠CDE的度数为____________
为等腰三角形,则∠CDE的度数为____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() );如果
);如果![]() ,那么(
,那么(![]() )
)![]() ,例如因为
,例如因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)= ,(7,1)= ,( ,81)=4.
(2)小明在研究这种运算时发现一个现象,(![]() ,
,![]() )=(3,4),小明给出了如下的证明:
)=(3,4),小明给出了如下的证明:
设(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即(3,4)![]() ,所以(
,所以(![]() ,
,![]() )=(3,4),请你尝试运用这种方法解决下列问题:
)=(3,4),请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=( , )(结果化成最简形式)
)=( , )(结果化成最简形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com