
【题目】规定两数![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() );如果
);如果![]() ,那么(
,那么(![]() )
)![]() ,例如因为
,例如因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)= ,(7,1)= ,( ,81)=4.
(2)小明在研究这种运算时发现一个现象,(![]() ,
,![]() )=(3,4),小明给出了如下的证明:
)=(3,4),小明给出了如下的证明:
设(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即(3,4)![]() ,所以(
,所以(![]() ,
,![]() )=(3,4),请你尝试运用这种方法解决下列问题:
)=(3,4),请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=( , )(结果化成最简形式)
)=( , )(结果化成最简形式)
【答案】(1)2,0,![]() ;(2)①见解析;②
;(2)①见解析;②![]() .
.
【解析】
(1)根据规定的两数之间的运算法则解答;
(2)①根据同底数幂的乘法法则,结合定义证明;
②根据例题和①中证明的式子作为公式进行变形即可.
解:(1)因为42=16,所以【4,16】=2.
因为70=1,所以【7,1】=0.
因为(±3)4=81,所以【±3,81】=4.
故答案为:2,0,±3;
(2)①证明:设【6,9】=x,【6,5】=y,则6x=9,6y=5,
∴5×9=45=6x6y=6x+y,
∴【6,45】=x+y,
则:【6,45】=【6,9】+【6,5】,
∴【6,45】-【6,9】=【6,5】;
②∵【3n,4n】=【3,4】,
∴【(x+1)m,(y-1)m】
=【(x+1),(y-1)】,【(x+1)n,(y-2)n】
=【(x+1),(y-2)】,
∴【(x+1)m,(y-1)m】+【(x+1)n,(y-2)n】,
=【(x+1),(y-1)】+【(x+1),(y-2)】,
=【(x+1),(y-1)(y-2)】,
=【(x+1),(y2-3y+2)】.
故答案为:(x+1),(y2-3y+2).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
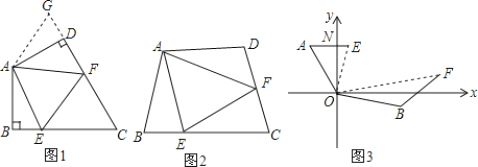
【题目】问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E、F分别是BC、CD上的点,且∠EAF=60°.为了探究图中线段BE,EF,FD之间的数量关系,小红的想法是:在EB的延长线上取一点G,使得BG=DF,连接AG,证明△ABG≌△ADF;再证明△AGE≌△AFE,从而得到结论,她的结论是_____________.
探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西40°的A处,舰艇乙在指挥中心南偏东80°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以50海里/小时的速度,同时舰艇乙沿北偏东50°的方向以70海里/小时的速度各自前进2小时后,在指挥中心观测到甲、乙两舰艇分别到达E,F处,两舰艇与指挥中心之间的夹角为70°,则此时两舰艇之间的距离为______海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某仓库原有商品300件,现记录了10天内该类商品进出仓库的件数如下所示(“+”表示进库,“-”表示出库)
+30,-10,-15,+25,+17,+35,-20,-15,+13,-35.
(1)请问经过10天之后,该仓库内的商品是增加了还是减少了?此时仓库还有多少商品?
(2)如果商品每次进出仓库需要人工搬运费是每件3元,请问这10天要付多少人工搬运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读型综合题
对于实数![]() 我们定义一种新运算
我们定义一种新运算![]() (其中
(其中![]() 均为非零常数),等式右边是通常的 四则运算,由这种运算得到的数我们称之为线性数,记为
均为非零常数),等式右边是通常的 四则运算,由这种运算得到的数我们称之为线性数,记为![]() ,其中
,其中![]() 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数 ![]() 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的![]() 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.
(1)若![]() ,则
,则![]() ,
,![]() ;
;
(2)已知![]() ,
,![]() .若正格线性数
.若正格线性数![]() ,(其中
,(其中![]() 为整数),问是否有满足这样条件的正格数对?若有,请找出;若没有,请说明理由.
为整数),问是否有满足这样条件的正格数对?若有,请找出;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
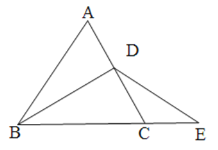
图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.
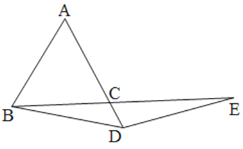
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线AP和点B,C,请用尺规按下列要求作图:
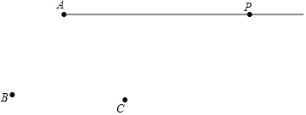
(1)连接AB,并在射线AP上截取AD=AB;
(2)连接BC、BD,并延长BC到E,使BE=BD.
(3)在(2)的基础上,取BE中点F,若BD=6,BC=4,求CF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com