
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
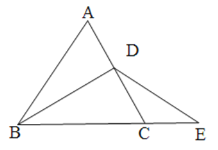
图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.
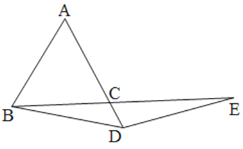
图2
【答案】(1)详见解析;(2)详见解析
【解析】
(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;解:(1)AD=CE,理由:过D作DF∥AB交BC于E,
(2)(1)中的结论仍成立,如图3,过点D作DP∥BC,交AB的延长线于点P,证明△BPD≌△DCE,得到PD=CE,即可得到AD=CE.
解:(1)AD=CE,
证明:如图1,过点D作DP∥BC,交AB于点P,
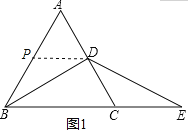
∵△ABC是等边三角形,
∴△APD也是等边三角形,
∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,
∵DB=DE,
∴∠DBC=∠DEC,
∵DP∥BC,
∴∠PDB=∠CBD,
∴∠PDB=∠DEC,
又∠BPD=∠A+∠ADP=120°,∠DCE=∠A+∠ABC=120°,
即∠BPD=∠DCE,
在△BPD和△DCE中,∠PDB=∠DEC,∠BPD=∠DCE,DB=DE,
∴△BPD≌△DCE,
∴PD=CE,
∴AD=CE;
(2)如图3,过点D作DP∥BC,交AB的延长线于点P,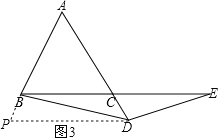
∵△ABC是等边三角形,
∴△APD也是等边三角形,
∴AP=PD=AD,∠APD=∠ABC=∠ACB=∠PDC=60°,
∵DB=DE,
∴∠DBC=∠DEC,
∵DP∥BC,
∴∠PDB=∠CBD,
∴∠PDB=∠DEC,
在△BPD和△DCE中,
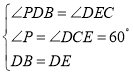
∴△BPD≌△DCE,
∴PD=CE,
∴AD=CE.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
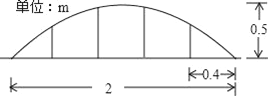
【题目】某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量![]() (毫克)随时间
(毫克)随时间![]() (小时)的变化情况如图所示,当成年人按规定剂量服药后.
(小时)的变化情况如图所示,当成年人按规定剂量服药后.

(1)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是________;
之间的函数关系式是________;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是______;
之间的函数关系式是______;
(3)如果每毫升血液中含药量![]() 毫克或
毫克或![]() 毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
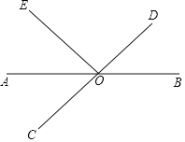
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=80°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com