
【题目】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量![]() (毫克)随时间
(毫克)随时间![]() (小时)的变化情况如图所示,当成年人按规定剂量服药后.
(小时)的变化情况如图所示,当成年人按规定剂量服药后.

(1)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是________;
之间的函数关系式是________;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是______;
之间的函数关系式是______;
(3)如果每毫升血液中含药量![]() 毫克或
毫克或![]() 毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)1≤x≤5.
;(3)1≤x≤5.
【解析】
(1)由图象可知x≤2时的图象是正比例函数,设y与x之间的函数关系式是y=kx,把(2,6)代入可求出k的值,即可得答案;
(2)由图象可知x≥2时的图象是一次函数,故设y与x之间的函数关系式是y=k1x+b,把(2,6)、(5,3)代入可求出k1和b的值,即可得答案;
(3)根据x≤2和x≥2时的解析式,分别求出y=3时x的值,可得y≥3时x的取值范围,即可得答案.
(1)设y与x之间的函数关系式是y=kx,
∵图象经过点(2,6),
∴6=2k,
解得:k=3,
∴x≤2时,y与x之间的函数关系式是y=3x.
故答案为:y=3x
(2)设y与x之间的函数关系式是y=k1x+b,
∵图象经过(2,6)、(5,3),
∴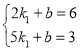 ,
,
解得:![]() ,
,
∴x≥2时,y与x之间的函数关系式是y=-x+8.
故答案为:y=-x+8
(3)当x≤2,y=3时,3=3x,即x=1,
当x≥2,y=3时,3=-x+8,即x=5,
由图象可知1≤x≤5时,y≥3,
∴这个有效时间范围是1≤x≤5小时,
故答案为:1≤x≤5


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC底边BC的长为4cm,面积为12cm,腰AB的垂直平分线交AB于点E,若点D为BC边的中点,M为线段EF上一动点,则△BDM的周长最小值为_________

查看答案和解析>>
科目:初中数学 来源: 题型:
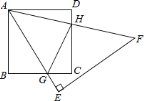
【题目】如图,正方形ABCD的面积为1cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两站的路程是312km,一列列车从甲站开往乙站,设列车的平均速度为xkm/h,所需时间为yh.
(1)试写出y关于x的函数关系式;
(2)2006年全国铁路第六次大提速前,这列列车从甲站到乙站需要4h,列车提速后,速度提高了26km/h,问提速后从甲站到乙站需要几个小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
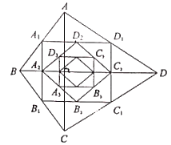
【题目】如图,四边形![]() 中,
中,![]() 顺次连接四边形
顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ,再顺次连接四边形
,再顺次连接四边形![]() 各边中点,得到四边形
各边中点,得到四边形![]() ...如此进行下去,得到四边形
...如此进行下去,得到四边形![]() 则下列结论正确的个数有( )
则下列结论正确的个数有( )
①四边形![]() 是矩形;②四边形
是矩形;②四边形![]() 是菱形;③四边形
是菱形;③四边形![]() 的周长为
的周长为![]() ; ④四边形
; ④四边形![]() 的面积是
的面积是![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题
材料一:《孟子》中记载有一尺之棰,日取其半,万世不竭,其中蕴含了“有限”与“无限”的关系.如果我们要计算到第n天时,累积取走了多长的木棒?可以用下面两种方法去解决:
方法一:第n天,留下了![]() 尺木棒,那么累积取走了
尺木棒,那么累积取走了![]() 尺木棒.
尺木棒.
方法二:第1天取走了![]() 尺木棒,第2天取走了
尺木棒,第2天取走了![]() 尺木棒,……第n天取走了
尺木棒,……第n天取走了![]() 尺木棒,那么累积取走了:
尺木棒,那么累积取走了:![]() 尺木棒.
尺木棒.
设:![]() ……①
……①
由①×![]() 得:
得:![]() ……②
……②
①-②得:![]() 则:
则:![]()
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问题:1+2+3+…+100=?据说当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确的答案:(1+100)+(2+99)+…+(50+51)=101×50=5050.
也可以这样理解:令S=1+2+3+4+…+100 ①,则S=100+99+98+…+3+2+1②
①+②得:2S=(1+100)+(2+99)+(3+98)+…+(100+1)=100×(1+100)
即![]()
请用你学到的方法解决以下问题:
(1)计算:![]() ;
;
(2)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层的2倍,问塔的顶层共有多少盏灯?
(3)某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动,某一周,这款软件的激活码为下面数学问题的答案:已知一列数1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,……其中第1项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,以此类推,求满足如下条件的正整数N:
,以此类推,求满足如下条件的正整数N:![]() ,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
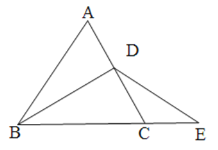
图1
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立,请说明理由.
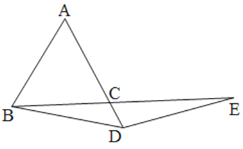
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
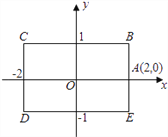
A. (2,0) B. (﹣1,1) C. (﹣2,1) D. (﹣1,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com