
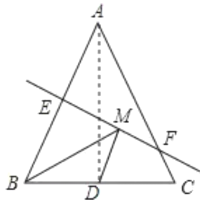
【题目】如图,等腰△ABC底边BC的长为4cm,面积为12cm,腰AB的垂直平分线交AB于点E,若点D为BC边的中点,M为线段EF上一动点,则△BDM的周长最小值为_________

【答案】8cm
【解析】
连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
解:如图,连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=![]() BCAD=
BCAD=![]() ×4×AD=12,
×4×AD=12,
解得:AD=6cm,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+![]() BC=6+
BC=6+![]() ×4=6+2=8cm.
×4=6+2=8cm.
故答案为:8cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
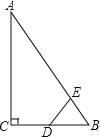
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
A.2B.2.5或3.5
C.3.5或4.5D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
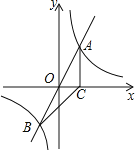
【题目】如图, 正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
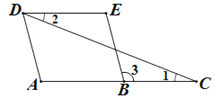
【题目】填空并填写理由:如图,AD∥BE,∠1=∠2,那么∠A与∠E相等吗?请完成解答过程:
解:∵AD∥BE(已知)
∠A=∠_____ (_________________)
又∵∠1=∠2 (______)
∴AC∥_____ (________________)
∴∠3=∠_____(两直线平行,内错角相等)
∴∠A=∠______ (_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
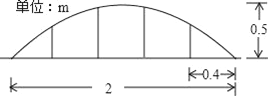
【题目】某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量![]() (毫克)随时间
(毫克)随时间![]() (小时)的变化情况如图所示,当成年人按规定剂量服药后.
(小时)的变化情况如图所示,当成年人按规定剂量服药后.

(1)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是________;
之间的函数关系式是________;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是______;
之间的函数关系式是______;
(3)如果每毫升血液中含药量![]() 毫克或
毫克或![]() 毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com