
【题目】如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.

【答案】(1)y=x2﹣4x﹣5,顶点坐标为D(2,﹣9);(2)①存在点P(3,﹣2)使四边形PEDF为平行四边形;②△PFH周长的最大值为![]() .
.
【解析】(1)利用待定系数法进行求解即可得;
(2)①求出直线BC解析式,表示PF,当PF=DE时,平行四边形存在.
②利用△PFH∽△BCO,应用相似三角形性质表示△PFH周长,应用函数性质讨论最值即可.
(1)把A(﹣1,0),B(5,0)代入抛物线y=ax2+bx﹣5,得
![]() ,解得:
,解得:![]() ,
,
∴y=x2﹣4x﹣5=(x-2)2-9,
∴顶点坐标为D(2,﹣9);
(2)①存在,
设直线BC的函数解析式为y=kx+b(k≠0),
把B(5,0),C(0,﹣5)代入得![]() ,解得:
,解得:![]() ,
,
∴BC解析式为y=x﹣5,
当x=m时,y=m﹣5,
∴P(m,m﹣5),
当x=2时,y=2﹣5=﹣3,
∴E(2.﹣3),
∵PF∥DE∥y轴,
∴点F的横坐标为m,
当x=m时,y=m2﹣4m﹣5,
∴F(m,m2﹣4m﹣5),
∴PF=(m﹣5)﹣(m2﹣4m﹣5)=﹣m2+5m,
∵E(2,﹣3),D(2,﹣9),
∴DE=﹣3﹣(﹣9)=6,
如图,连接DF,
∵PF∥DE,
∴当PF=DE时,四边形PEDF为平行四边形,
即﹣m2+5m=6,
解得m1=3,m2=2(舍去),
当m=3时,y=3﹣5=2,
此时P(3,﹣2),
∴存在点P(3,﹣2)使四边形PEDF为平行四边形;
②由题意,在Rt△BOC中,OB=OC=5,
∴BC=5![]() ,
,
∴C△BOC =10+5![]() ,
,
∵PF∥DE∥y轴,
∴∠FPE=∠DEC=∠OCB,
∵FH⊥BC,
∴∠FHP=∠BOC=90°,
∴△PFH∽△BCO,
∴![]() ,
,
即C△PFH=![]() ,
,
∵0<m<5,
∴当m=﹣![]() 时,△PFH周长的最大值为
时,△PFH周长的最大值为![]() .
.



科目:初中数学 来源: 题型:
【题目】冬季降至,贫困山区恶劣的地理环境加之其落后的交通条件,无疑将使得山区在漫长冬季里物资更加匮乏,“让冬天不冷让爱心永驻”,重庆市公益组织心驿家号召全市人民为贫困山区的孩子们捐赠过冬衣物,本次捐赠共收集了11600件棉衣、7500件羽绒服及防寒服若干,自愿者将所有衣物分成若干A、B、C类组合,由自愿者们分别送往交通极其不便利的各个山区,一个A类组合含有60件棉衣,80件防寒服和50件羽绒服;一个B类组合含有40件棉衣,40件防寒服;一个C类组合含有40件棉衣,60件防寒服,50件羽绒服;求防寒服一共捐赠了_____件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区进行课堂教学改革,将学生分成5个学习小组,采取团团坐的方式.如图所示,这是某校八(1)班教室简图,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别代表五个学习小组的位置.已知
分别代表五个学习小组的位置.已知![]() 点的坐标为(-1,3).
点的坐标为(-1,3).
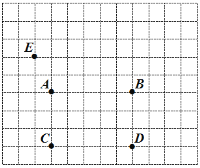
(1)请按题意建立平面直角坐标系(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度),写出图中其他几个学习小组的坐标;
(2)若(1)中建立的平面直角坐标系坐标原点为![]() ,点
,点![]() 在
在![]() 的延长线上,请写出
的延长线上,请写出![]() 、
、![]() 、
、![]() 之间的等量关系,并说明原因.
之间的等量关系,并说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保障人畜饮水安全,某县急需饮水设备12台,现有甲、乙两种设备可供选择,已知购买1台甲种设备和2台乙两种设备共需10000元,购买3台甲种设备和1台乙两种设备共需15000元,且甲种设备的安装及运输费用为600元/台,乙种设备的安装及运输费用为800元/台.
(1)购买1台甲、乙两种设备各需多少元?
(2)若购买的费用不超过40000元,安装及运输费用不超过9200元,则有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一元二次方程![]() 中,若系数
中,若系数![]() 和
和![]() 可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
可在0,1,2,3中取值,则其中有实数解的方程的个数是___ 个,写出其中有两个相等实数根的一元二次方程_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元

(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() );如果
);如果![]() ,那么(
,那么(![]() )
)![]() ,例如因为
,例如因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)= ,(7,1)= ,( ,81)=4.
(2)小明在研究这种运算时发现一个现象,(![]() ,
,![]() )=(3,4),小明给出了如下的证明:
)=(3,4),小明给出了如下的证明:
设(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即(3,4)![]() ,所以(
,所以(![]() ,
,![]() )=(3,4),请你尝试运用这种方法解决下列问题:
)=(3,4),请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=( , )(结果化成最简形式)
)=( , )(结果化成最简形式)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com