【题目】如图，某人为了测量小山顶上的塔ED的高，他在山下的点A处测得塔尖点D的仰角为45°，再沿AC方向前进60 m到达山脚点B，测得塔尖点D的仰角为60°，塔底点E的仰角为30°，求塔ED的高度．(结果保留根号)
【答案】塔高约为(60＋20
)m.
【解析】试题先求出∠DBE=30°，∠BDE=30°，得出BE=DE，然后设EC=x，则BE=2x，DE=2x，DC=3x，BC=
x，然后根据∠DAC=45°，可得AC=CD，列出方程求出x的值，然后即可求出塔DE的高度．
试题解析：由题知，∠DBC=60°，∠EBC=30°，∴∠DBE=∠DBC﹣∠EBC=60°﹣30°=30°．
又∵∠BCD=90°，∴∠BDC=90°﹣∠DBC=90°﹣60°=30°，∴∠DBE=∠BDE，∴BE=DE．
设EC=x，则DE=BE=2EC=2x，DC=EC+DE=x+2x=3x，BC=
=
=x，由题知，∠DAC=45°，∠DCA=90°，AB=20，∴△ACD为等腰直角三角形，∴AC=DC，∴x+60=3x，解得：x=
，∴DE=2x=
．
答：塔高约为m．
科目：初中数学 来源： 题型：
【题目】如图1是一种折叠式可调节的鱼竿支架的示意图，AE是地插，用来将支架固定在地面上，支架AB可绕A点前后转动，用来调节AB与地面的夹角，支架CD可绕AB上定点C前后转动，用来调节CD与AB的夹角，支架CD带有伸缩调节长度的伸缩功能，已知BC=60cm．
（1）若支架AB与地面的夹角∠BAF=35°，支架CD与钓鱼竿DB垂直，钓鱼竿DB与地面AF平行，则支架CD的长度为 cm（精确到0.1cm）；（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）．
（2）如图2，保持（1）中支架AB与地面的夹角不变，调节支架CD与AB的夹角，使得∠DCB=85°，若要使钓鱼竿DB与地面AF仍然保持平行，则支架CD的长度应该调节为多少？（结果保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】利用配方法求出抛物线
的顶点坐标、对称轴、最大值或最小值；若将抛物线先向左平移
个单位，再向上平移
个单位，所得抛物线的函数关系式为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,某人在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i为1∶
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.则A,B两点间的距离是( )
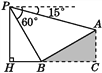
A. 15米 B. 20
米 C. 20
米 D. 10
米
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解下列各题：
(1)先化简，再求代数式(
的值，其中x＝
cos30°＋
；
(2)已知α是锐角，且sin(α＋15°)＝
.计算
－4cosα－(π－3.14)0＋tanα＋(
)－1的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
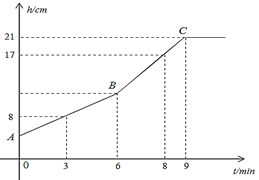
【题目】某兴趣小组观察下雨天学校池塘水面高度h(单位：cm)与观察时间t(单位：min)的关系，并根据当天观察数据画出了如图所示的图象，请你结合图象回答下列问题：
(1)求线段BC的表达式；
(2)试求出池塘原有水面的高度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，二次函数y＝x2－2x－3的图象与x轴交于A，B两点，与y轴交于点C，连接BC，点D为抛物线的顶点，点P是第四象限的抛物线上的一个动点(不与点D重合)．
(1)求∠OBC的度数；
(2)连接CD，BD，DP，延长DP交x轴正半轴于点E，且S△OCE＝S四边形OCDB，求此时P点的坐标；
(3)过点P作PF⊥x轴交BC于点F，求线段PF长度的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．
实验与探究：
（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（﹣2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′ 、C′ ；
归纳与发现：
（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为 ；
运用与拓广：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
四点在一条直线上，
，
.老师说：再添加一个条件就可以使
.下面是课堂上三个同学的发言，甲说：添加
；乙说：添加
；丙说：添加
.
（1）甲、乙、丙三个同学说法正确的是________
（2）请你从正确的说法中选择一种，给出你的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com