
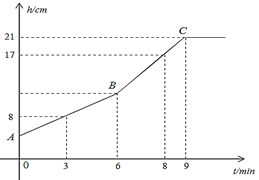
【题目】某兴趣小组观察下雨天学校池塘水面高度h(单位:cm)与观察时间t(单位:min)的关系,并根据当天观察数据画出了如图所示的图象,请你结合图象回答下列问题:
(1)求线段BC的表达式;
(2)试求出池塘原有水面的高度.
【答案】(1)y=4x-15;(2)6
【解析】
(1)设直线BC的解析式为y=kx+b(k≠0),然后利用待定系数法求出直线BC线段的解析式即可;
(2)根据(1)求出B点的坐标,然后求出直线AC的解析式,令x为零即可求出池塘原有水面的高度.
解:(1)设直线BC的解析式为y=kx+b(k≠0)
∵点(9,21)与(8,17)在直线BC上
∴![]()
解得:![]()
∴直线BC的解析式为y=4x-15;
(2)由(1)知直线BC的解析式为y=4x-15
设点B为(6,y)
∴y=4×6-15=9
设直线AB的解析式为y=k1x+b1(k≠0)
∵点(6,9)与(3,8)在直线AB上
∴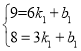
解得: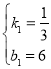
∴直线AB的解析式为y=![]() x+6
x+6
则令x=0有y=6
∴池塘原有水面的高度为6厘米.
故答案为:(1)y=4x-15;(2)6


科目:初中数学 来源: 题型:
【题目】如图,已知直线AB:y=![]() x+
x+![]() 分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )
分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为( )

A. (0,4) B. (0,5) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BE⊥AC于E,且D、E分别是AB、AC的中点,延长BC至点F,使CF=CE.
(1)∠ABC的度数.
(2)求证:BE=FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5。一只蚂蚁如果要沿着长方体的表面从点A爬到点B,爬行的最短路程是( )
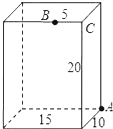
A.25B.![]() C.35D.无法确定
C.35D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
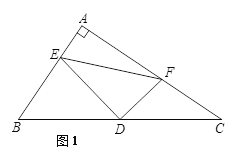

(1)如图1,试说明![]() ;
;
(2)如图2,若AB=AC,BE=12,CF=5,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点A在反比例函数y=![]() (k≠0)的图象上,点D在y轴上,点B、点C在x轴上.若平行四边形ABCD的面积为10,则k的值是( )
(k≠0)的图象上,点D在y轴上,点B、点C在x轴上.若平行四边形ABCD的面积为10,则k的值是( )
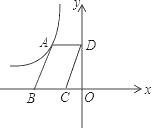
A. ﹣10 B. ﹣5 C. 5 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
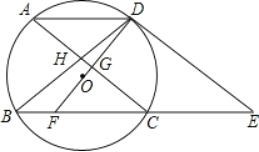
【题目】如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5cm,AC=8cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com